In hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism.Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them.A space-fitting model of this structure, called hexagonal closed-packed (HCP), is constitution of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible Three spheres are then placed over the first layer so that they touch each other and represent the second layer.Each one of these three spheres touches three spheres of the bottom layer.Finally, the second layer is covered with third layer that is identical to the bottom layer in relative position.Assume radius of even sphere to be 'r'.
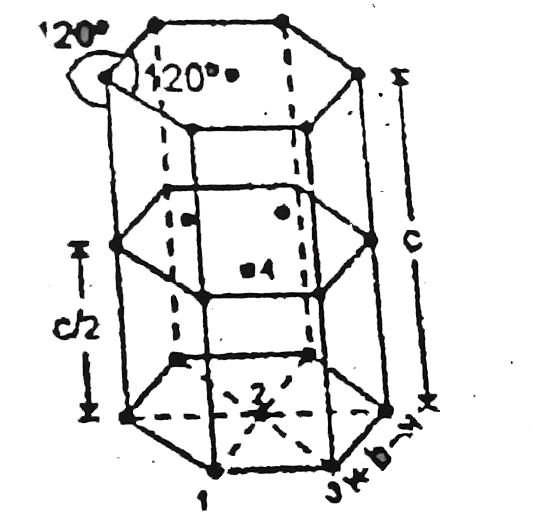
In hcp lattice, if a plane is drawn parallel to layers A and B at a distance c8 above the layer B, it passes through centres of x tetrahedral and y octahedral voids.A plane parallel to layer A at a distance c8 just below it passes through centres of p tetrahedral and q octahedral voids.Find (x+y+p+q) c is the cell parameter of hcp lattice, the vertical edge length.

10
9
6
14
The correct Answer is:A
x=7, y=0,p=3,q=0
Topper's Solved these Questions
Similar Questions
In hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The empty space in this HCP unit cell is :
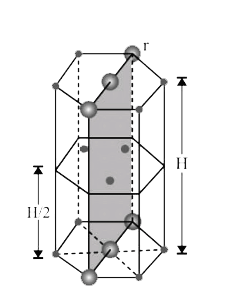
View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The volume of this HCP unit cell is

View Solution
Knowledge Check
In hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism.Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them.A space-fitting model of this structure, called hexagonal closed-packed (HCP), is constitution of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible Three spheres are then placed over the first layer so that they touch each other and represent the second layer.Each one of these three spheres touches three spheres of the bottom layer.Finally, the second layer is covered with third layer that is identical to the bottom layer in relative position.Assume radius of even sphere to be 'r'.
The volume of this HCP unit cell is :
 A12√2r3B24√2r3C16√2r3D643√3r3
A12√2r3B24√2r3C16√2r3D643√3r3In hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagon and three atoms are sandwiched in between them. A space filling model of this structure, called hexagonal close packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical sphere as closely as possible. Three spheres are then placed over the first layer so that they touch other and represent the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be same
The volume of this HCP unit cell isA24√2r3B16√2r3C12√2r3D643√3r3In hexagonal systems of crystals, a frequently ecounted arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are reqular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. There spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three sphere touches three spheres of the bottom layer. Finally the second layer is covered with third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be 'r'

The volume of this HCP unit cell isA24√2r3B16√2r3C12√2r3D643√3r3
In hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (hcp), is constitued of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touched three spheres of the bottom layer. Finally, the second layer is convered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be 'r'.
The volume of this hcp unit cell is
View SolutionIn hexagonal systems of crystals, a frequently ecounted arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are reqular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. There spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three sphere touches three spheres of the bottom layer. Finally the second layer is covered with third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be 'r'

The number of atoms in the HCP unit cell is
View SolutionIn hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagon and three atoms are sandwiched in between them. A space filling model of this structure, called hexagonal close packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical sphere as closely as possible. Three spheres are then placed over the first layer so that they touch other and represent the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be same
The number of atoms in this HCP unit cell is
View SolutionIn hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagon and three atoms are sandwiched in between them. A space filling model of this structure, called hexagonal close packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical sphere as closely as possible. Three spheres are then placed over the first layer so that they touch other and represent the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be same
The empty space in this HCP unit cell is
View SolutionIn hexagonal system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space -filling model of this structure, called hexagonal close-packed (HCP), is consituted of a sphere on a flat surface surrouneded in the same plane by six identical spheres as closely possible. Three sphere are then palces over the first layer so that they touch each other and represent second layer is covered with third layer that is identical to the bottom layer in relative position. Assume radius of enery sphere to be r.

The number of atoms in the HPC unit cell is :
View Solution
