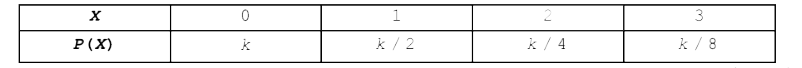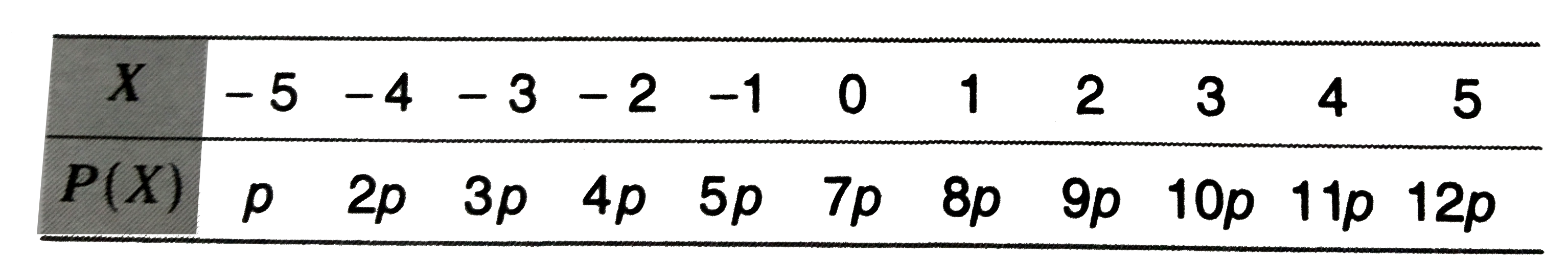The probability distribution of a random variable X is given below
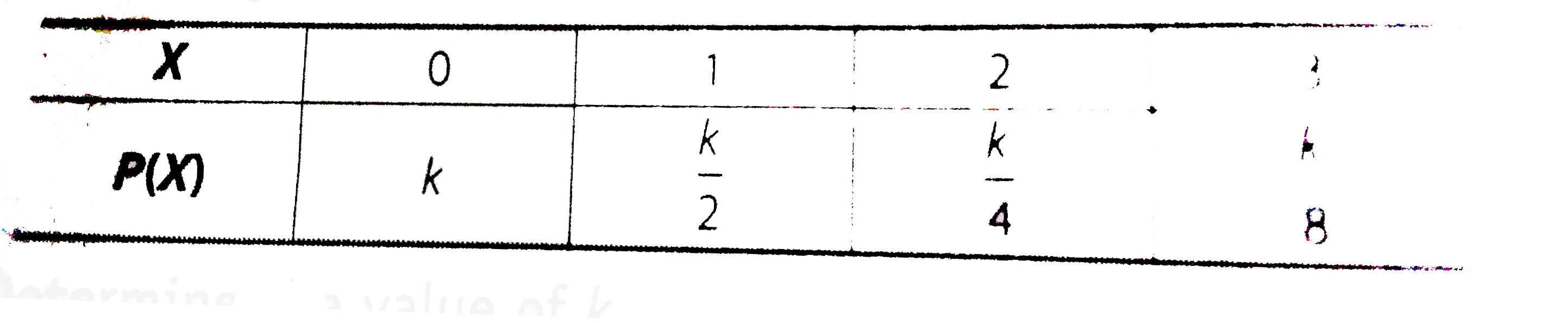
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).
Video Solution
Text Solution
We have,
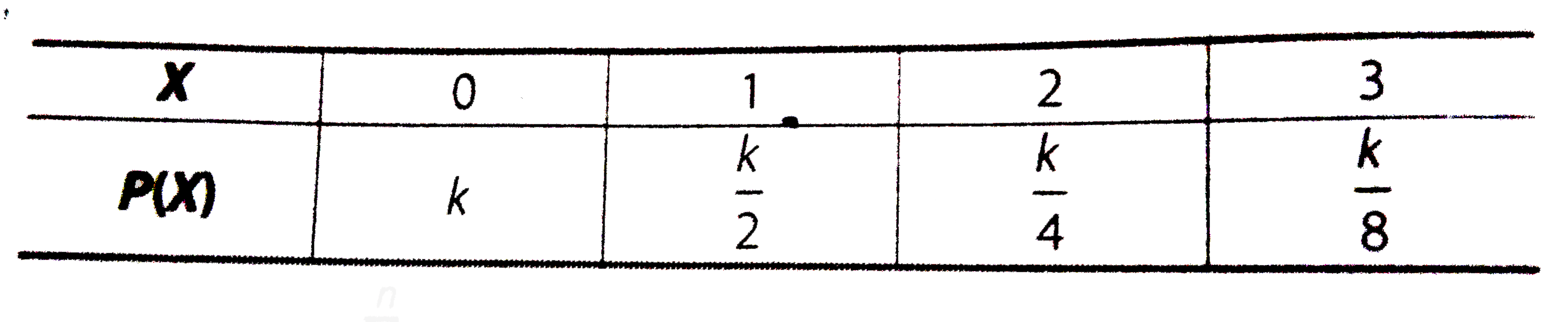
(i) Since, n∑i=1Pi=1,i=1,2,…..,nandPi≥0
∴k+k2+k4+k8=1
⇒8k+4k+2k+k=8
∴k=815
(ii) P(X≤2)=P(0)+P(1)+P(2)=k+k2+k4
=(4k+2k+k)4=7k4=74⋅815=1415
and P(X>2)=P(3)=k8=18⋅815=115
(iii) P(X≤2)+P(X≥2)=1415+115=1
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The probability distribution of a discrete random variable X is given below
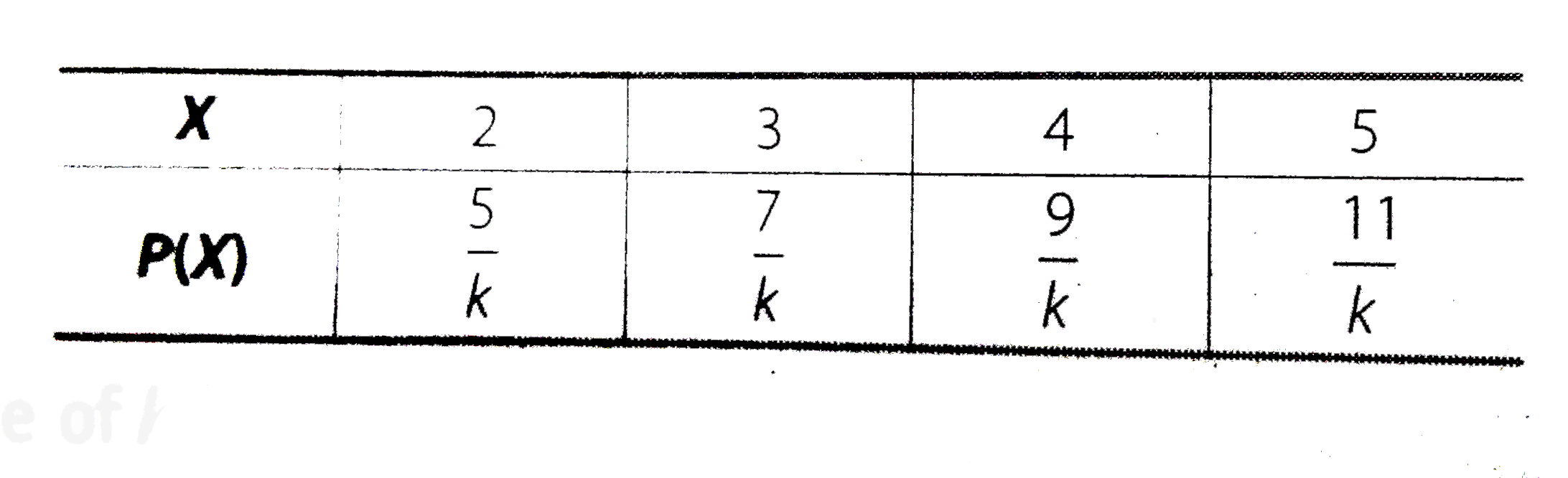
The value of k isA8B16C32D48 - Question 2 - Select One
The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2
probability distribution of a random variable X is
If a=P(X≥2)andb=P(X<3) then
 View Solution
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)View SolutionThe probability of a random variable X is given below
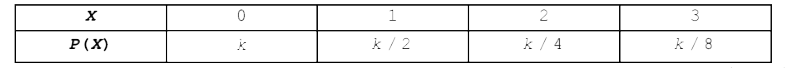
Find P(X≤2)+P(X>2)View SolutionIf the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View Solution