A biased die is such that P(4)=110 and other scores being equally likely. The die tossed twice. If X is the number of four seen, then find the variance of the random variable X.
since, X= Number of fours seen
On tossing twi die, X=0,1,2.
Also, P4=110andP(not4)=910
So, P(X=0)=P((not4))⋅P(not4)=910⋅910=81100
P(X=1)=P((not4))⋅P(4)+P4⋅P(not4)=910⋅110+110⋅910=18100
P(X=2)=P(4)⋅P(4)=110⋅110=1100
Thus, we get folllowing table
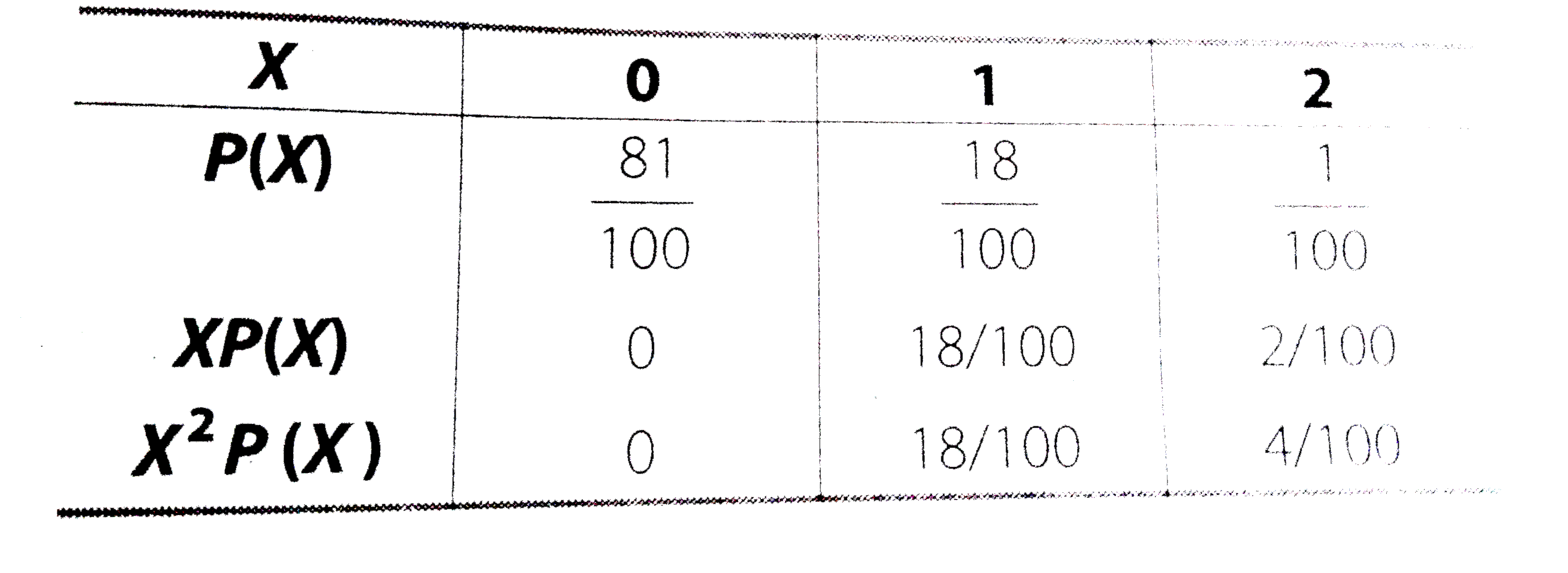
∴ Var (X)=E(X2)−[E(X)]2=∑X2P(X)−[∑XP(X)]2
=[0+18100+4100]−[0+18100+2100]2
=22100−(20100)2=1150−125
=11−250=950=18100=0.18
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A die is rolled .IF X denotes the number of positive divisors of the outcome then the range of the random variable X is
A{1,2,3}B{1,2,3,4}C{1,2,3,5,6,}D(1,3,5} - Question 2 - Select One
A die is thrown thrice. A success is or 6 in a throw. Find the mean and variance of the number of successes.
Aμ=1,σ2=2/3Bμ=2/3,σ2=1Cμ=2,σ2=2/3Dnone - Question 3 - Select One
A die is tossed twice. The prbability of having a number greater than 4 on each toss is
A13B19C23D112
A die is thrown three times. Let X be the number of twos seen. Find the expectation of X .
View SolutionIf the variance of the random variable X is 9 the S.D .of the random variable -4X+8 is
View SolutionA die is tossed twice A success is getting an odd number on a toss. Find the variance of the number of successes.
View SolutionA die is loaded in such a way that an even number is twice likely to occur as an odd number. If the die is tossed twice, find the probability distribution of the random variable X representing the perfect squares in the two tosses.
View SolutionTwo baised dice are thrown together. For the first die P(6)=12 , other scores being equally likely while for the second die, P(1)=25 and other scores are equally likely. Find the probability distribution of the number of ones seen.
View Solution

