AP is tangent to circle O at point P, What is the length of OP?
Let the radius of given circle is r.
∴ OP=OB=r
∴ OA=2+r, OP=r, AP=4
∴ OP=OB=r
∴ OA=2+r, OP=r, AP=4
∠OPA=90∘ (radius through point of contact is perpendicular to the tangent)
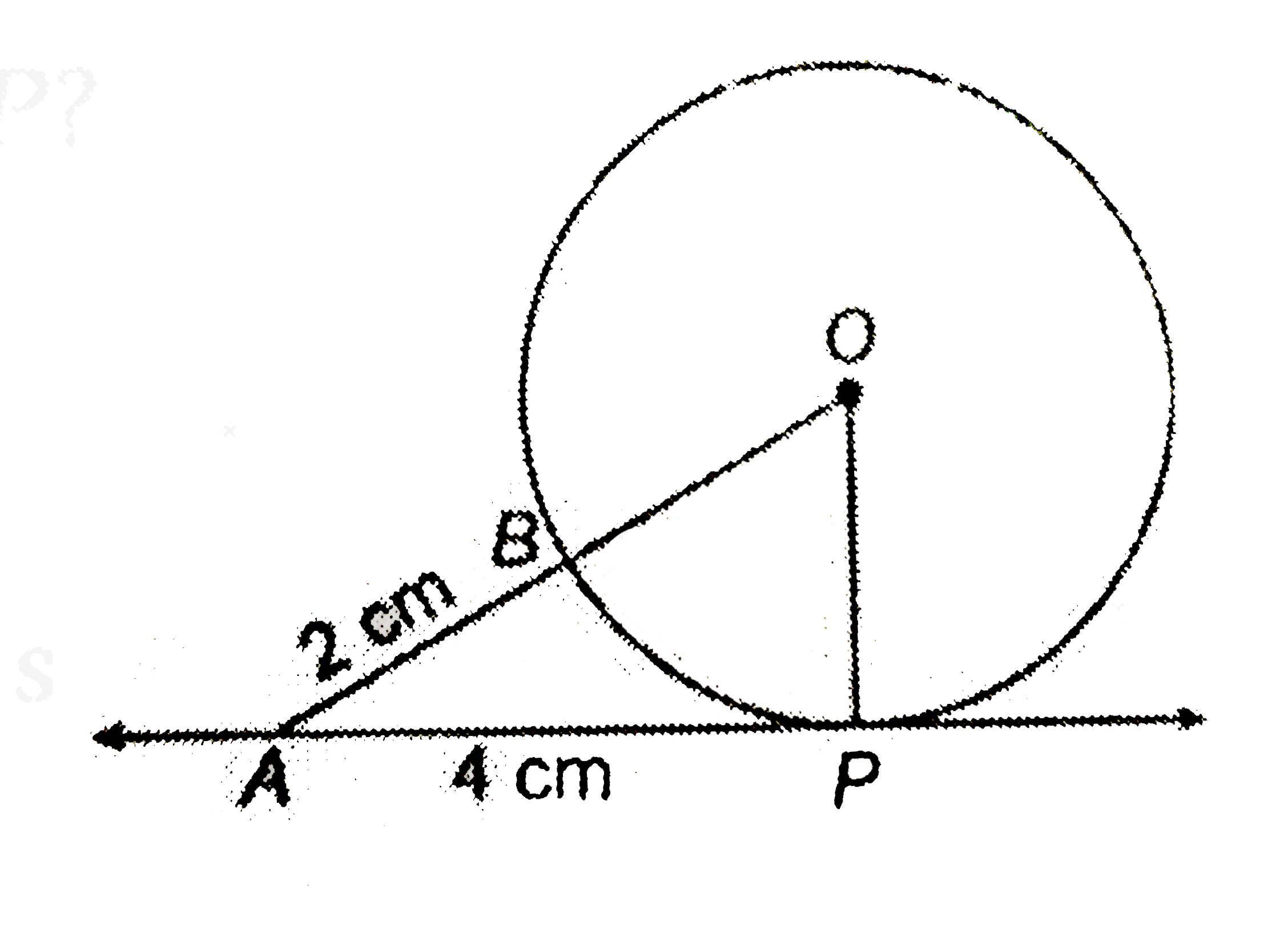
∴ In right △OPA,
OA2=OP2+AP2 (by Pythagoras theorem)
(2+r2)=r2+(4)2
⇒ 4+r2+4r=r2+16
(2+r2)=r2+(4)2
⇒ 4+r2+4r=r2+16
⇒ 4r=12 ⇒ r=3
∴ OP=3cm.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar11videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise25videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
Similar Questions
Draw a circle of radius 3 cm. Mark a point P on the circle. Draw tangent to the circle through point P using the centre of the circle Analysis
A circle of radius 3 cm can be drawn. Let the cemntre of the given circle be O and line l be the required tangent
We know, converse of tangent theorem states that , 'A line perpendicular to radius at its outer end is tangent .
∴ We construct perpendicular to radius OP at point, then line l is the required tangent .
 View Solution
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.View Solution
Knowledge Check
- Question 1 - Select One
A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−a - Question 2 - Select One
2 equal tangents PA and PB are drawn from an external point P on a circle with centre O. What is the length of each tangent, if P Is 12 cm from the centre and the angle between the tangents is 120∘ ?
A24 cm.B6 cm.C8 cm.DCannot be determined - Question 3 - Select One
AP is tangent to the circle with centre O at point A. OP =10 cm and ∠OPA=30∘. The radiu of the circle is
A10 cmB5√3cmC5 cmD10√3cm
In the figure,O is the centre of the circle PQ is the tangent at point P then what is the measure of ∠OPQ ?Why ?
 View Solution
View SolutionIn the figure given below, two equal chords cut at point P. If AB = CD = 10 cm, OC = 13 cm (O is the centre of the circle) and PB = 3 cm, then what is the length of OP ?
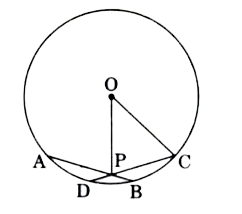 View Solution
View SolutionTwo circles of unequal radii have four common tangents. A transverse common tangent meets the direct common tangents at the points P & Q. If length of direct tangent (between the point of contacts) is 8 then length of PQ is
View SolutionTwo tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionO is the centre of a circle. There is a point P in the region of the circle. If PA = PB = PC where A, B and C are points on the circumference of the circle, then OP must be equal to :
View Solution

