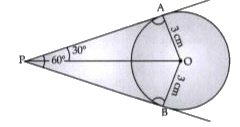
If two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then
find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles
triangle, then find ∠OQP.
To solve the first part of the question, we need to find the length of each tangent drawn to a circle of radius 3 cm, where the two tangents are inclined at an angle of 60 degrees.
1. Understanding the Geometry:
- We have a circle with center O and radius 3 cm.
- Let A and B be the points where the tangents touch the circle, and C be the point from which the tangents are drawn.
- The angle between the two tangents (∠ACB) is given as 60 degrees.
2. Using the Properties of Tangents:
- The radius at the point of contact is perpendicular to the tangent. Therefore, ∠OAC = 90 degrees and ∠OBC = 90 degrees.
- Since the tangents are drawn from the same external point C, the lengths of the tangents CA and CB are equal.
3. Finding the Angles:
- Since the tangents are inclined at 60 degrees, we can divide this angle into two equal parts: ∠CAB = ∠CBA = 30 degrees.
4. Applying the Right Triangle:
- In triangle OAC, we have:
- OA = radius = 3 cm
- OC = length of the tangent (which we will denote as x)
- ∠OAC = 90 degrees
- ∠CAB = 30 degrees
5. Using Trigonometric Ratios:
- In triangle OAC, we can use the tangent function:
tan(30∘)=OAAC=3x
- We know that tan(30∘)=1√3, so we can set up the equation:
1√3=3x
6. Cross Multiplying:
- Cross multiplying gives us:
x=3√3 cm
7. Conclusion:
- Therefore, the length of each tangent is 3√3 cm.
- We have a circle with center O and radius 3 cm.
- Let A and B be the points where the tangents touch the circle, and C be the point from which the tangents are drawn.
- The angle between the two tangents (∠ACB) is given as 60 degrees.
- The radius at the point of contact is perpendicular to the tangent. Therefore, ∠OAC = 90 degrees and ∠OBC = 90 degrees.
- Since the tangents are drawn from the same external point C, the lengths of the tangents CA and CB are equal.
- Since the tangents are inclined at 60 degrees, we can divide this angle into two equal parts: ∠CAB = ∠CBA = 30 degrees.
- In triangle OAC, we have:
- OA = radius = 3 cm
- OC = length of the tangent (which we will denote as x)
- ∠OAC = 90 degrees
- ∠CAB = 30 degrees
- In triangle OAC, we can use the tangent function:
tan(30∘)=OAAC=3x
- We know that tan(30∘)=1√3, so we can set up the equation:
1√3=3x
- Cross multiplying gives us:
x=3√3 cm
- Therefore, the length of each tangent is 3√3 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3cm then the length of each tangent is
A3cmB3√32cmC3√3cmD6cmPQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isoceless triangle, then ∠OQP is equal to
A30∘B45∘C60∘D90∘IF two tangents inclined at an angle of 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to
A3√32 cmB6 cmC3 cmD3√3cm
If two tangents inlined at an angle 60∘ are drawn to a circle of radius 3 cm , then the length of each tangent is equal to :
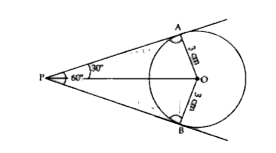
View SolutionIf two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then what is the length of each tangent ?
View SolutionTwo tangents making an angle of 60∘ between them, are drawn to a circle of radius √2 cm, then find the length of each tangent.
View SolutionPQ is a tangent to a circle with centre O at the point P . If OPQ is an isosceles triangle, then ∠OQP is equal to 30o (b) 45o (c) 60o (d) 90o
View SolutionIf two tangents inclined at an angle of 60∘ are drawn to a circle of radius 4 cm, then the length of each tangent is equal to :
View Solution