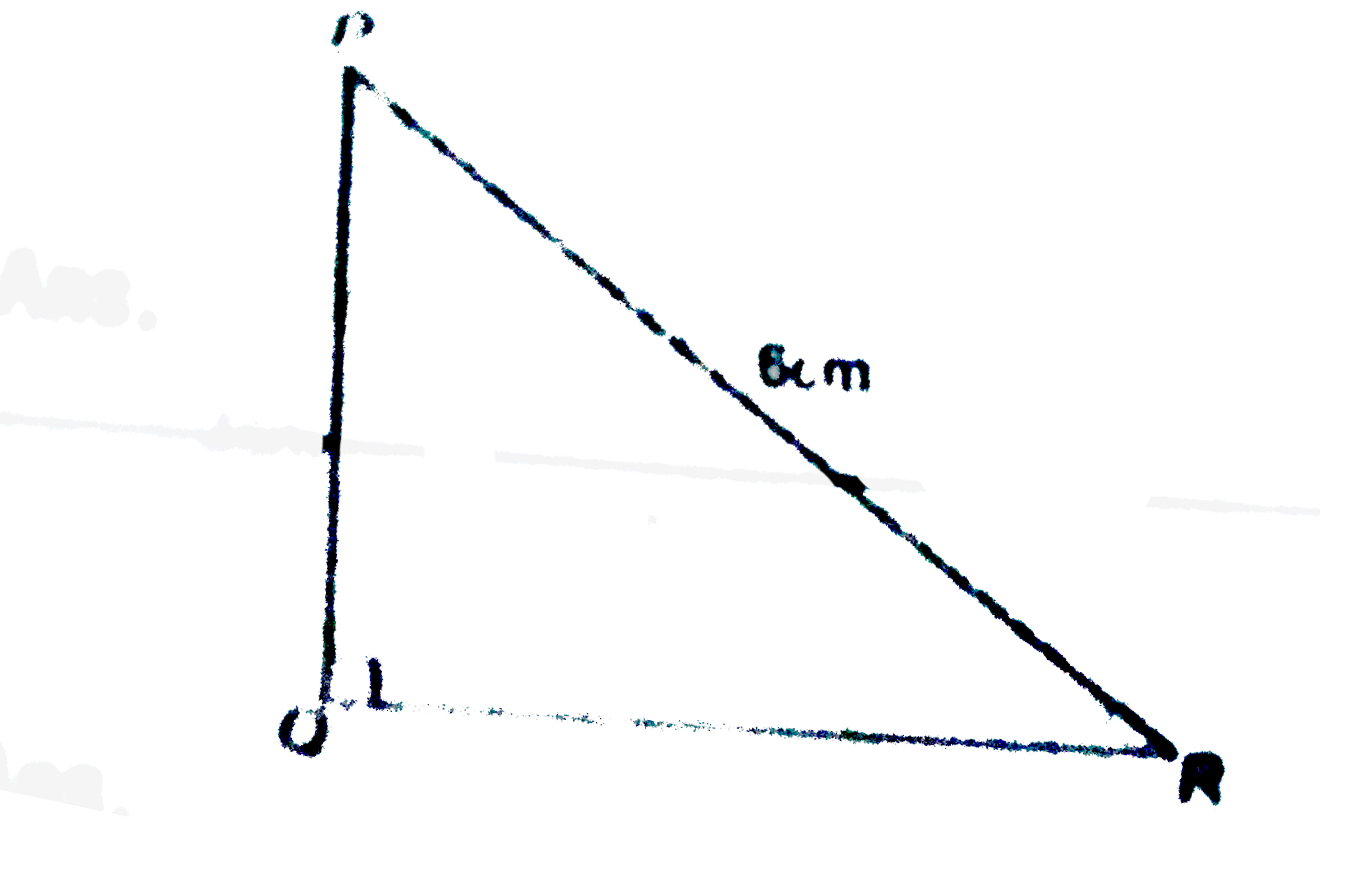
In PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
InΔPQR
cos<QPR=PQPR=36=12=cos60∘
⇒<QPR=60∘
and sin<PRQ=PQPR=36=12
⇒sin<PRQ=sin30∘
⇒<PRQ=30∘
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a20videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8 B22videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions5videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - PROBLEMS FROM NCERT/ EXEMPLAR10videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions8videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
In △PQR , right-angled at Q, PQ=3cm and PR=6cm . Determine ∠P and ∠R .
View SolutionIn ΔPQR,right-angled at Q (see figure), PQ = 3 cm and PR = 6 cm. Determine ∠QPRand ∠PRQ
View SolutionIn ΔOPQ, right-angled at P, OP = 7 cm andOQ − PQ = 1 cmDetermine the values of sin Q and cos Q.
View SolutionIn Fig. 4.230, each of PA, QB, RC and SD is perpendicular to l . If AB=6cm , BC=9cm , CD=12cm and PS=36cm , then determine PQ, QR and RS . (FIGURE)
View SolutionIn ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=4cm, PB=6cm and PQ=3cm , determine BC .
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
 View Solution
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 View Solution
View SolutionIn a ABC , P and Q are point on the sides AB and AC respectively, such that PQBC . If AP=2.4cm , AQ=2cm , QC=3cm and BC=6cm , find AB and PQ .
View SolutionIn Fig. 4.177, ACBAPQ . If BC=10cm, PQ=5cm, BA=6.5cm and AP=2.8cm find CA and AQ . Also, find the area (ACB):area (APQ) . (FIGURE)
View Solution

