The angle of depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the ship and tower.
The correct Answer is:50√3m
To find the horizontal distance between the ship and the tower, we can use the concept of trigonometry, specifically the tangent function, which relates the angle of depression to the opposite and adjacent sides of a right triangle.
1. Identify the Components:
We have a tower of height AB=50 m. The angle of depression from the top of the tower to the ship is 30∘.
2. Draw the Diagram:
Draw a right triangle where:
- A is the top of the tower.
- B is the base of the tower (ground level).
- C is the position of the ship.
- The angle ACB is the angle of depression, which is 30∘.
- The height AB is the opposite side (50 m), and the horizontal distance BC is the adjacent side.
3. Use the Angle of Depression:
The angle of depression from point A to point C is equal to the angle CAB (alternate interior angles). Therefore, CAB=30∘.
4. Set Up the Tangent Function:
Using the definition of tangent in the right triangle:
tan(θ)=oppositeadjacent
Here, θ=30∘, the opposite side is AB=50 m, and the adjacent side is BC:
tan(30∘)=ABBC=50BC
5. Calculate tan(30∘):
We know that:
tan(30∘)=1√3
6. Set Up the Equation:
Substitute tan(30∘) into the equation:
1√3=50BC
7. Cross-Multiply:
Cross-multiplying gives:
BC=50⋅√3
8. Final Calculation:
Therefore, the horizontal distance BC between the ship and the tower is:
BC=50√3 meters
Final Answer:
The horizontal distance between the ship and the tower is 50√3 meters.
---
We have a tower of height AB=50 m. The angle of depression from the top of the tower to the ship is 30∘.
Draw a right triangle where:
- A is the top of the tower.
- B is the base of the tower (ground level).
- C is the position of the ship.
- The angle ACB is the angle of depression, which is 30∘.
- The height AB is the opposite side (50 m), and the horizontal distance BC is the adjacent side.
The angle of depression from point A to point C is equal to the angle CAB (alternate interior angles). Therefore, CAB=30∘.
Using the definition of tangent in the right triangle:
tan(θ)=oppositeadjacent
Here, θ=30∘, the opposite side is AB=50 m, and the adjacent side is BC:
tan(30∘)=ABBC=50BC
We know that:
tan(30∘)=1√3
Substitute tan(30∘) into the equation:
1√3=50BC
Cross-multiplying gives:
BC=50⋅√3
Therefore, the horizontal distance BC between the ship and the tower is:
BC=50√3 meters
The horizontal distance between the ship and the tower is 50√3 meters.
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (short Answer Questions)
5 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Revision Exercise (long Answer Questions)
1 Video
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Long Answer Questions
5 Videos
- REAL NUMBERSBOOK - NAGEEN PRAKASHANCHAPTER - REAL NUMBERSEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
Similar Questions
The angle if depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the boat and the bridge.
View SolutionThe height of a light house is 40 m. The angle of depression of a ship from the top of the light house is 60∘. Find the distance of ship from the light house.
View Solution
Knowledge Check
The angle of depression of a ship from the top of a 30 m hight tower is 60∘. The distance of ship from the base of the tower is
A30mB30√3mC10√3mD10mTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
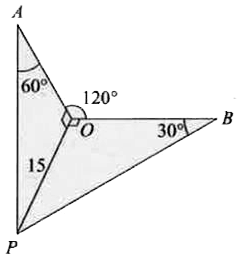 A5√39 mB5√30 mC5√21 mD5√3 m
A5√39 mB5√30 mC5√21 mD5√3 m
The angle of depression of 47 m high building form the top of a tower 137 m high is 30∘ . Calculate the distance between the building and the tower .
View SolutionThe angle of depression between a flying kite and 'a' point on the ground is 60 m. If the string makes 30∘. Find the horizontal distance between the ship and tower.
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also the height of the other tower.
View SolutionFrom the top of a platform, the angle of elevation of a tower was 30∘. The tower was 45 m high and the horizontal distance between the platform and the tower was 40√3 m. What was the height of the platform?
View SolutionThe angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top of the second tower from the foot of the first tower is 30∘. Find the distance between the two and also the height of the tower.
View SolutionThe angle of depression of the foot of a building from the top of a tower 30 m away is 30∘. How high is the tower?
View Solution
