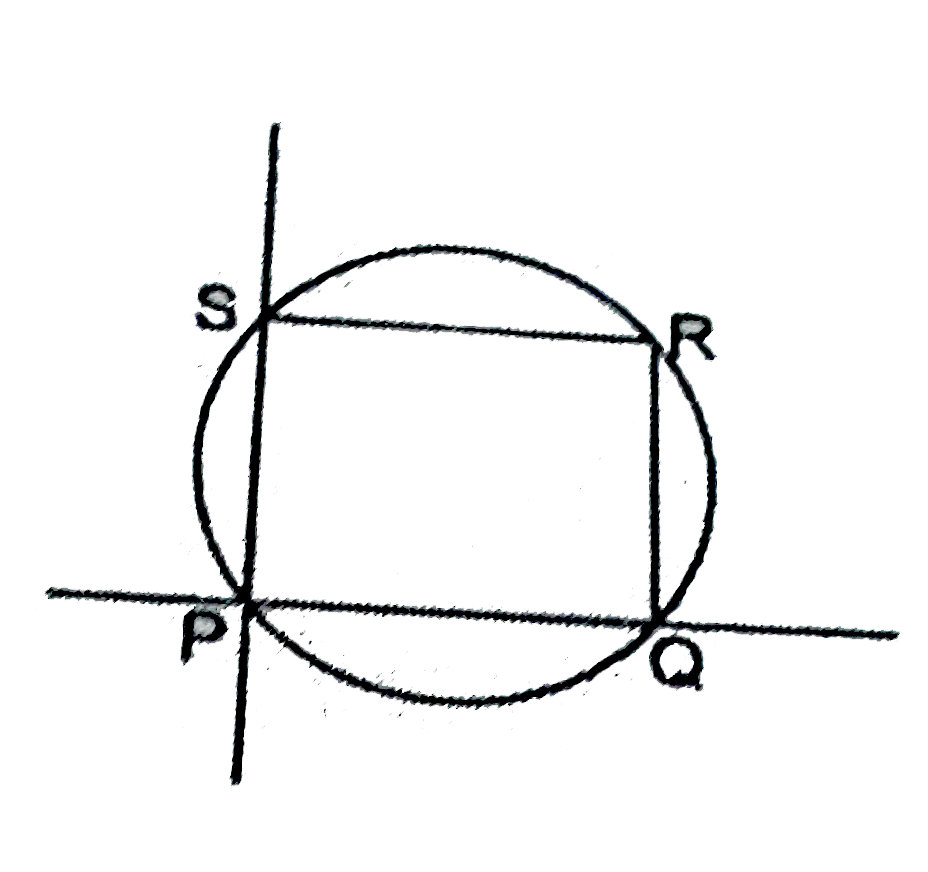
PQRS is a square of side 'b'. Prove that the equation of circumcircle of square PQRS, where PQ and PS are the axes, is x2+y2=b(x+y).
Draw a square of side 'b' taking PS as the axes. Now the co-ordinates of its vertices are P(0,0),Q(b,0),R(b,b)andS(0,b)
From the equation of circumcircle of square PQRS,
(x1,y1)=(0,0)and(x2,y2)=(b,b)
Equation of circle
(x−x1)(x−x2)+(y−y1)(y−y2)=0
⇒(x−0)(x+b)+(y−0)(y−b)=0
⇒x2−bx+y2−by=0
⇒x2+y2=b(x+y).
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CONIC SECTIONEXERCISE - Miscellaneous Example3videos
CONIC SECTION
- BOOK - NAGEEN PRAKASHANCHAPTER - CONIC SECTIONEXERCISE - Exercise 11A38videos
CONIC SECTION
- BOOK - NAGEEN PRAKASHANCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - MISCELLANEOUS EXERCISE20videos
COMPLEX NUMBERS AND QUADRATIC EQUATION
- BOOK - NAGEEN PRAKASHANCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise6videos
INTRODUCTION OF THREE DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
Equation of circumcircle of square OACB of side a, where
OA and OB are along coordinate axes , isAx2+y2−ax+ay=0Bx2+y2+ax−ay=0Cx2+y2+ax+ay=0Dx2+y2−ax−ay=0 - Question 2 - Select One
The sides of a square are x=4,x=7,y=1 and y=4 . The equation of the circumcircle of the square is :
Ax2+y2+11x=4y+17=0Bx2+y2+7x−6y+18=0Cx2+y2−11x−3y+30=0Dx2+y2−11x−5y+32=0 - Question 3 - Select One
Solve for x and y.
x+y=a+b
ax−by=a2−b2Ax=b,y=−bBx=b,y=aCx=−a,y=−bDx=a,y=b
The equation of the circumcircle of the triangle, the equation of whose sides are y=x,y=2x,y=3x+2, is
View Solutionfind (a) the area (b) the perimeter of the square PQRS, if the side is 20 cm.
View SolutionIf tangents PQandPR are drawn from a variable point P to thehyperbola x2a2−y2b2=1,(a>b), so that the fourth vertex S of parallelogram PQSR lies on the circumcircle of triangle PQR , then the locus of P is x2+y2=b2 (b) x2+y2=a2 x2+y2=a2−b2 (d) none of these
View SolutionThe sides of a square are x=2,x=3,y=1andy=2. Find the equation of the circle drawn on the diagonals of the square as its diameter.
View SolutionIf sides of a square is (x+2y-z) units then the area of the square is.......
View Solution

