Two concentric circles are such that the smaller divides the larger into two regions of equal area. If the radius of the smaller circle is 2, then the length of the tangent from any point 'P'on the larger circle to the smaller circle is
Step by step video & image solution for Two concentric circles are such that the smaller divides the larger into two regions of equal area. If the radius of the smaller circle is 2, then the length of the tangent from any point 'P'on the larger circle to the smaller circle is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
सिद्ध कीजिए कि दो सकेन्द्रीय वृतों में बड़े वृत्त की वे जीवा जो छोटे वृत्त को स्पर्श करती हैं, समान लम्बाई की होती हैं।
View Solution5 व 3 सेमी वाले त्रिज्या के दो सकेन्द्रीय वृत्त हैं बड़े वृत्त कि उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हैं।
View Solutionसिद्ध करें की दो संकेन्द्रिय वृतों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती हैं वह स्पर्श बिंदु पर समद्विभाजित हो जाती हैं|
View Solutionदो सकेंद्रीय व्रतों (concentric circles) में सिद्ध करो कि बड़े वृत्त की वह जीवा जोकि छोटे वृत्त को स्पर्श करती हैं , स्पर्श बिंदु पर समद्विभजित होती है।
View SolutionTwo circles have radius 5 and 26. The smaller circle passes through centre of the larger one. What is the difference between the lengths of the longest and shortest chords of the larger circle that are tangent to the smaller circle?
View SolutionThe difference between the radii of a smaller circle and a larger circle is 7cm and the difference between the areas of the two circles is 1078sq.cm. Find the radius of the smaller circle.
View SolutionA circle is drawn in a sectore of a larger circle of radius r, as shown in fugure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the smaller circle is
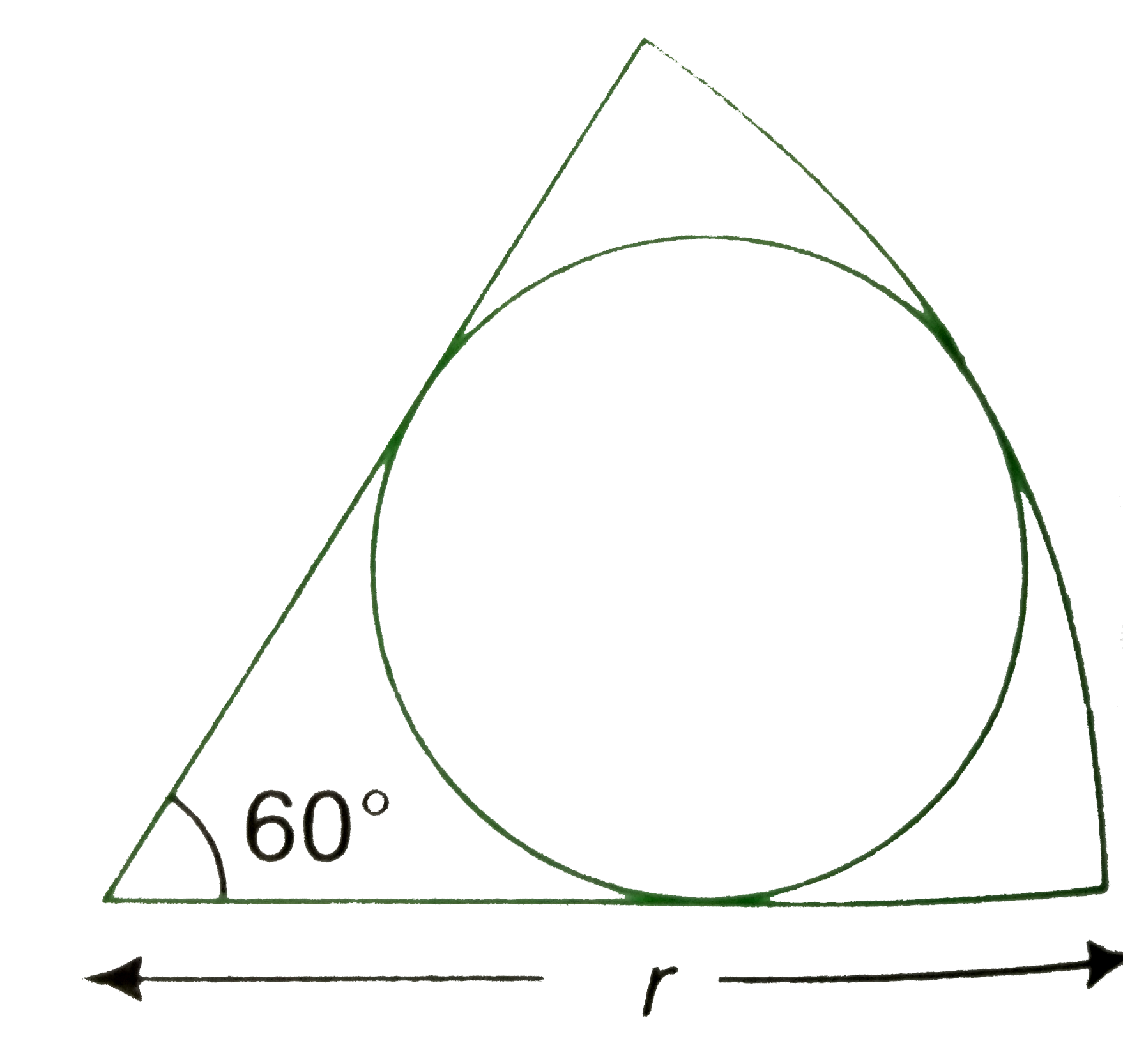
View SolutionIn two concentric circles, a chord of length 24cm of larger circle becomes a tangent to the smaller circle whose radius is 5cm. Find the radius of the larger circle.
View Solution
