The velocity of a particle at an instant is 10ms−1. After 3 s its velocity will becomes 16ms−1. The velocity at 2 s, before the given instant will be
6ms−1
4ms−1
2ms−1
1ms−1
The correct Answer is:A
To find the velocity of the particle at 2 seconds before the given instant, we can follow these steps:
Step 1: Identify the given values
- Initial velocity (u) at the given instant (t = 0): u=10m/s
- Final velocity (v) after 3 seconds: v=16m/s
- Time interval (t): t=3s
Step 2: Calculate the acceleration
Using the formula for acceleration:
a=v−ut
Substituting the known values:
a=16m/s−10m/s3s=6m/s3s=2m/s2
Step 3: Find the velocity at t=−2s (2 seconds before the given instant)
We need to find the initial velocity (u') at t=−2s. We can use the kinematic equation:
v=u+at
Rearranging the equation to find u′:
u′=v−at
At t=2s before the given instant, the time interval for acceleration will be:
t=2s
Substituting the values:
u′=10m/s−(2m/s2×2s)=10m/s−4m/s=6m/s
Conclusion
The velocity of the particle at 2 seconds before the given instant is 6m/s.
---
- Initial velocity (u) at the given instant (t = 0): u=10m/s
- Final velocity (v) after 3 seconds: v=16m/s
- Time interval (t): t=3s
Using the formula for acceleration:
a=v−ut
Substituting the known values:
a=16m/s−10m/s3s=6m/s3s=2m/s2
We need to find the initial velocity (u') at t=−2s. We can use the kinematic equation:
v=u+at
Rearranging the equation to find u′:
u′=v−at
At t=2s before the given instant, the time interval for acceleration will be:
t=2s
Substituting the values:
u′=10m/s−(2m/s2×2s)=10m/s−4m/s=6m/s
The velocity of the particle at 2 seconds before the given instant is 6m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Relative Velocity
Explore 18 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Higher Order Thinking Skills
Explore 10 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Acceleration
Explore 19 Videos
- MOTION IN A PLANE Book:NCERT FINGERTIPSChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The velocity of a projectile at the initial point A is (2 i+3 j)m/s .Its velocity (in m/s ) at point B is
View SolutionIn the given figure , if the velocity of the block C at a particular instant is −20ms−1ˆJ , then the velocity of the rod (A) that instant will be : (string is attached to wedge )
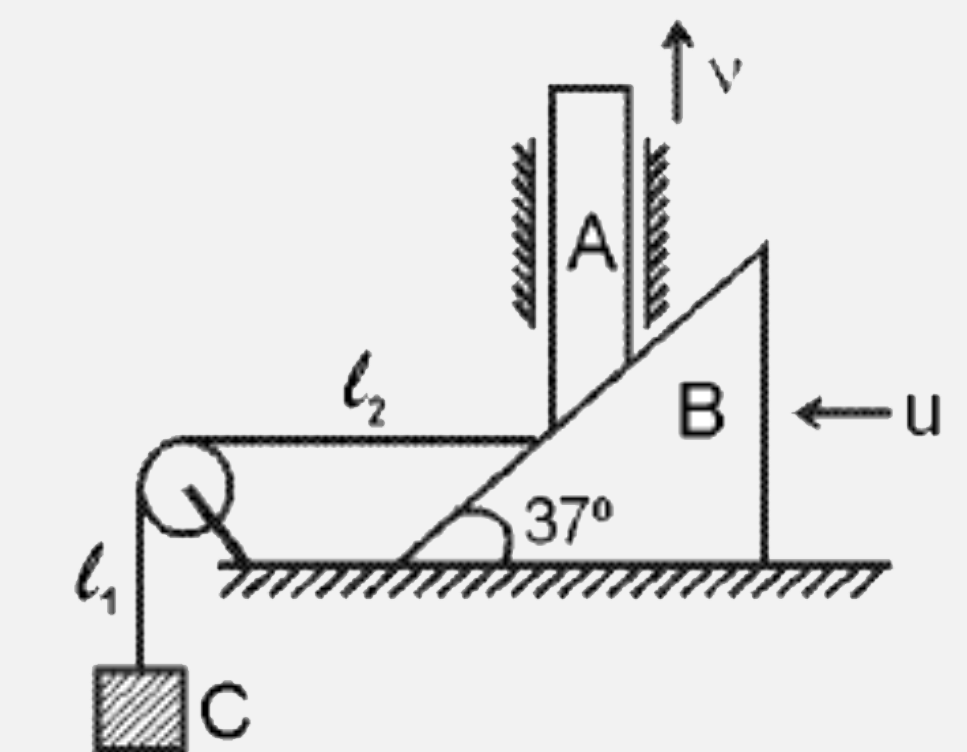
View Solution
Knowledge Check
The velocity of a particle at an instant is 10 m/s. After 5 s, the velocity of the particle is 20 m/s. The velocity at 3 s before the instant when the velocity of the particle was 10 m/s is
A8 m/sB6 m/sC4 m/sD7 m/sThe velocity of a particle at an instant is 10m/s. After 5sec, the velocity of the particle is 20m/s. Find the velocity at 3 seconds before from the instant when velocity of a particle is 10m/s.
A8m/sB4m/sC6m/sD7m/sThe velocity of A at an instant is 4m/s rightwards. Then the velocity of block B is
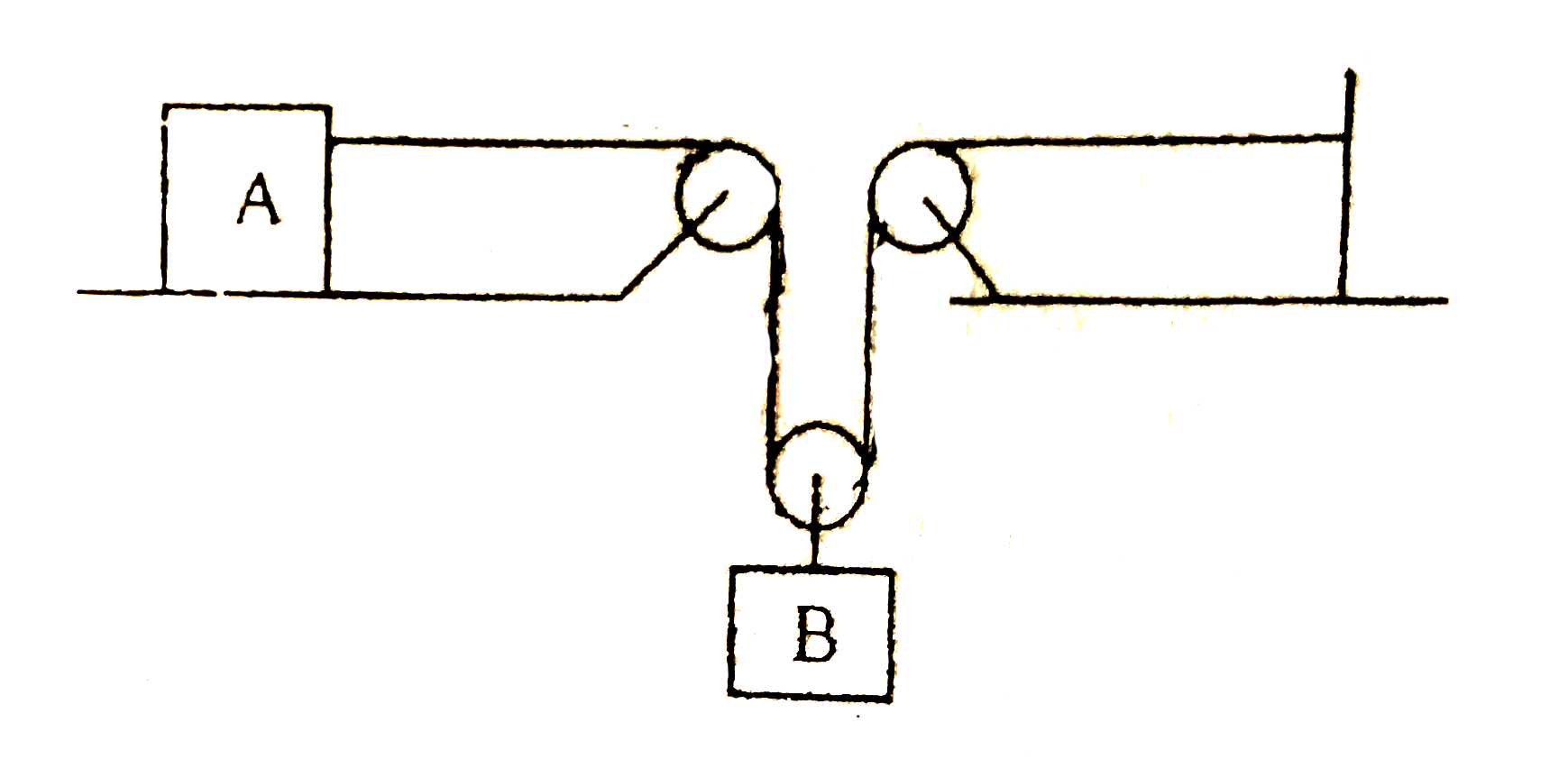 A4m/s downwardsB2m/s upwardsC2m/s downwardsD1m/s upwards
A4m/s downwardsB2m/s upwardsC2m/s downwardsD1m/s upwards
The velocity of the particle at any time t is given by vu=2t(3−t)ms−1. At what time is its velocity maximum?
View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)m/s. Its velocity (in m/s) at point B is

View SolutionThe velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View SolutionIf the velocity of a particle is given by v=(180−16x)12ms, then its acceleration will be
View SolutionThe velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
View Solution