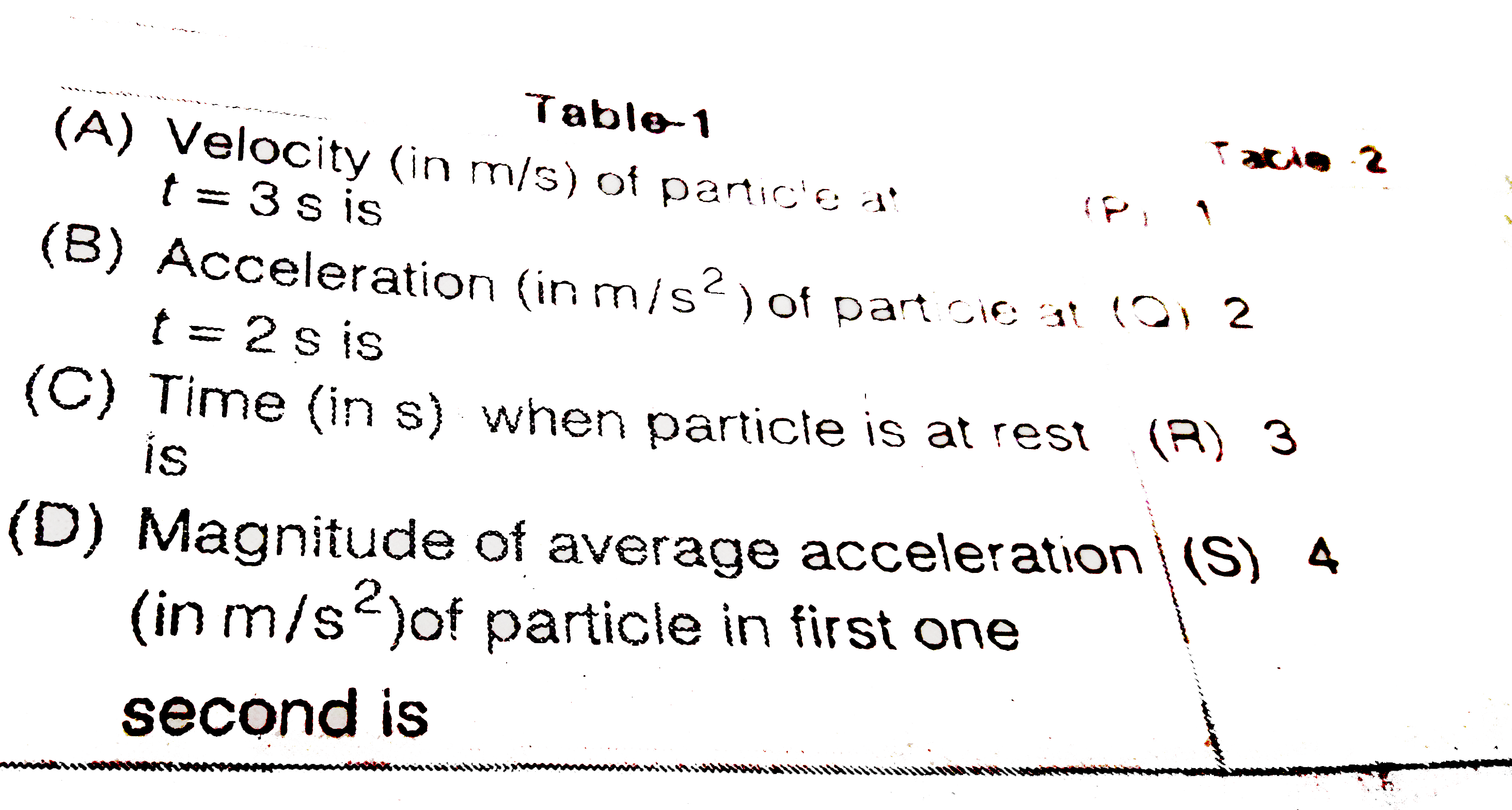The velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
1s
(log 10)s
2 (log 10)s
10 s
The correct Answer is:B
To solve the problem step by step, we will start from the given information about the velocity of the particle and derive the time taken to cover a distance of 9 meters.
Step 1: Understand the relationship between velocity, distance, and time.
The velocity v of the particle is given by the equation:
v=s+1
where s is the distance traveled in meters and t is the time in seconds.
Step 2: Relate velocity to distance and time.
We know that velocity can also be expressed as the derivative of distance with respect to time:
v=dsdt
Thus, we can set up the equation:
dsdt=s+1
Step 3: Rearrange the equation for integration.
We can rearrange the equation to separate variables:
dss+1=dt
Step 4: Integrate both sides.
Now, we will integrate both sides. The left side integrates with respect to s and the right side with respect to t:
∫dss+1=∫dt
The left side integrates to:
ln|s+1|=t+C
where C is the constant of integration.
Step 5: Solve for the constant of integration.
To find the constant C, we need an initial condition. However, since we are only interested in the time taken to cover a distance of 9 meters, we can proceed without finding C explicitly.
Step 6: Substitute the distance into the equation.
We need to find the time t when the distance s=9 meters:
ln|9+1|=t+C
This simplifies to:
ln10=t+C
Step 7: Determine the time taken.
Since we do not have an initial condition, we can express the time taken as:
t=ln10−C
However, for our purposes, we can assume C=0 for simplicity, so:
t=ln10
Final Answer:
The time taken by the particle to cover a distance of 9 meters is:
t=ln10 seconds
The velocity v of the particle is given by the equation:
v=s+1
where s is the distance traveled in meters and t is the time in seconds.
We know that velocity can also be expressed as the derivative of distance with respect to time:
v=dsdt
Thus, we can set up the equation:
dsdt=s+1
We can rearrange the equation to separate variables:
dss+1=dt
Now, we will integrate both sides. The left side integrates with respect to s and the right side with respect to t:
∫dss+1=∫dt
The left side integrates to:
ln|s+1|=t+C
where C is the constant of integration.
To find the constant C, we need an initial condition. However, since we are only interested in the time taken to cover a distance of 9 meters, we can proceed without finding C explicitly.
We need to find the time t when the distance s=9 meters:
ln|9+1|=t+C
This simplifies to:
ln10=t+C
Since we do not have an initial condition, we can express the time taken as:
t=ln10−C
However, for our purposes, we can assume C=0 for simplicity, so:
t=ln10
The time taken by the particle to cover a distance of 9 meters is:
t=ln10 seconds
Topper's Solved these Questions
Similar Questions
Knowledge Check
The displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
A2m/s2B4m/s2C6m/s2D8m/s2Velocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
A3π[2−√32]B[2−√32]C2π[2−√32]D4π[2−√32]The velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :A2mB3mC4mD6m
The speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionThe instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
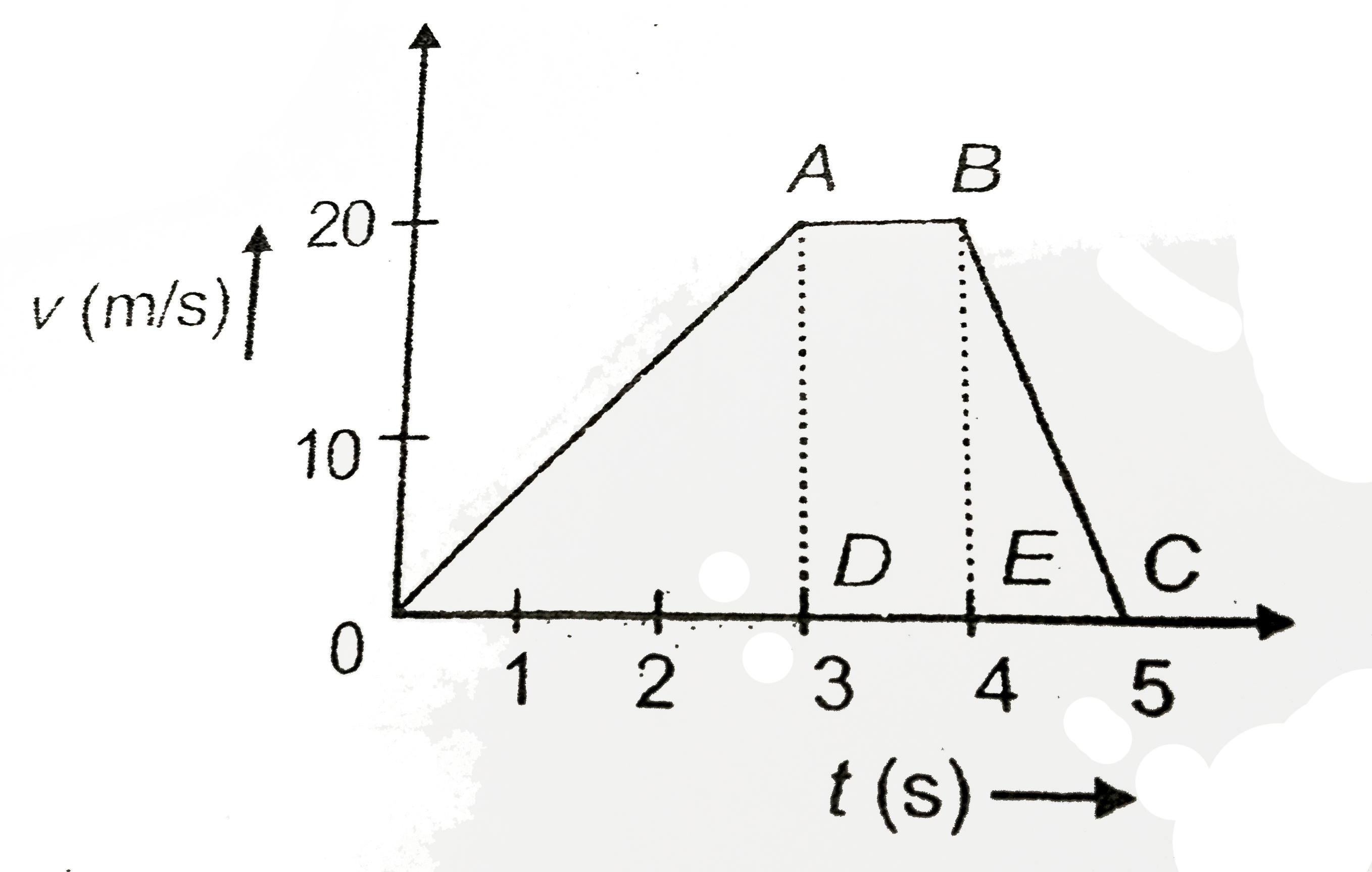
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View Solution