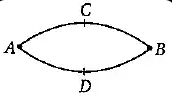
A length of path ACB is 1500 m and the length of the path ADB is 2100 m. Two particles start from point A simultaneously around the track ACBDA. One of them travels the track in clockwise sense and other in anti-clockwise sense and other in anti-clockwise with their respective constant speeds. After 12 s from the start, the first time they meet at the point B. After minimum time (in s) in which they meet first at point B, again will they meet at the point B is time $t_{min} = {(12)}^{x} s$ .The value of x is

A

2

B

3

C

4

D

5

Text Solution

Verified by Experts

The correct Answer is:(a)

The velocity of first particle is $v_{1} = \frac{1500}{12} m s^{- 1}$ and the velocity of second particle is $v_{2} = \frac{2100}{12} m s^{- 1}$ . Let after completing $n_{1}$ and $n_{2}$ trips, they will again meet at the point B.
$∴$ $\frac{3600 n_{1}}{v_{1}} = \frac{3600 n_{2}}{v_{2}}$ = t
[total path length $= 1500 + 2100 = 3600$ ]
or $\frac{n_{1}}{n_{2}} = \frac{v_{1}}{v_{2}} = \frac{\frac{1500}{12}}{\frac{2100}{12}} = \frac{1500}{2100} = \frac{5}{7}$
$∴ t_{min} = 3600 \times \frac{5}{v_{1}}$
$3600 \times \frac{5}{1500} \times 12 = 144 s = {(12)}^{x}$
$∴$ x = 2

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A man is facing towards the east. He then turns anti-clockwise, again anti-clockwise and then clock wise. In which direction is he facing now?
AWest
BNorth
CSouth
DEast
Question 2 - Select One
Two particles A and B execute SHM on a straight line of path length 2 m starting from the two extreme points simultaneously. If their respective time periods are 1 s and 2 s, the minimum time in which they meet is
A $\frac{1}{4} s$
B $\frac{1}{3} s$
C $\frac{1}{2} s$
D $\frac{2}{5} s$

NCERT FINGERTIPS-MOTION IN A STRAIGHT LINE-Higher Order Thinking Skills

Home
Ask Doubt
Profile