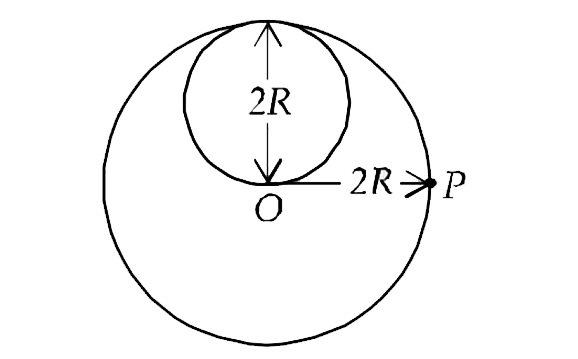
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO to the nearest integer is
13/37
37/13
73/31
8/13
The correct Answer is:B
Let M be mass of the whold disc.
then, the mass of the removed disc =Mπ(2R)2πR2=M4
So, moment of inertia of the remaining disc about an axis passing through O
IO=12M(2R)2−[12(M4)R2+M4R2]
2MR2−[MR2+2MR28]=MR2[2−38]=138MR2
Moment of the inertia of the remaining disc about an axis passing throuth P is
IP=12M(2R)2+M(2R)2]−[12(M4)R2+M4(√5R2)
=2MR2+4MR2−[MR28+5MR24]
=6MR2−118MR2=378MR2
∴IPIO=378×813=3713
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - NCERT Exemplar8videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason15videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Rolling Motion16videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 350videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendiucalr to the plane of the lamina. The ratio IPIO ot the nearest integer is
 View Solution
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A square lamina is as shown in figure. The moment of inertia of the frame about the three axes as shown in figure I1,I2andI3 respectively. Select the correct alternative.
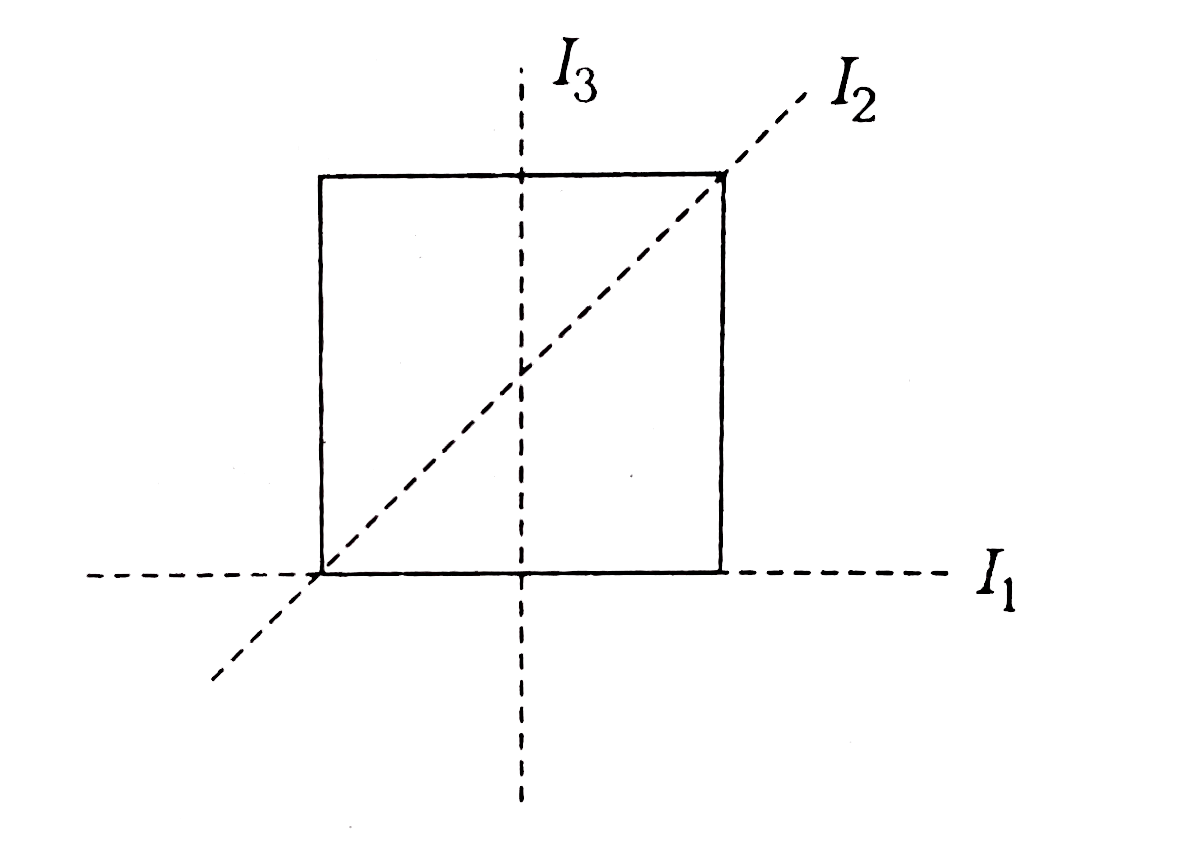 AI2=I2>I1BI1>I2>I3CI2=I3<I1DI1<I2<I3
AI2=I2>I1BI1>I2>I3CI2=I3<I1DI1<I2<I3 - Question 2 - Select One
A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
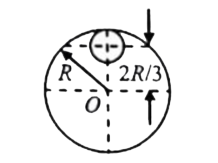 A4MR2B9MR2C379MR2D409MR2
A4MR2B9MR2C379MR2D409MR2 - Question 3 - Select One
The masses of two uniform discs are in the ratio 1:2 and their diameters in the ratio 2:1. The ratio of their moment, of inertia about the axis passing through their respective centres and perpendicular to their planes is
A1:1B1:2C2:1D1:4
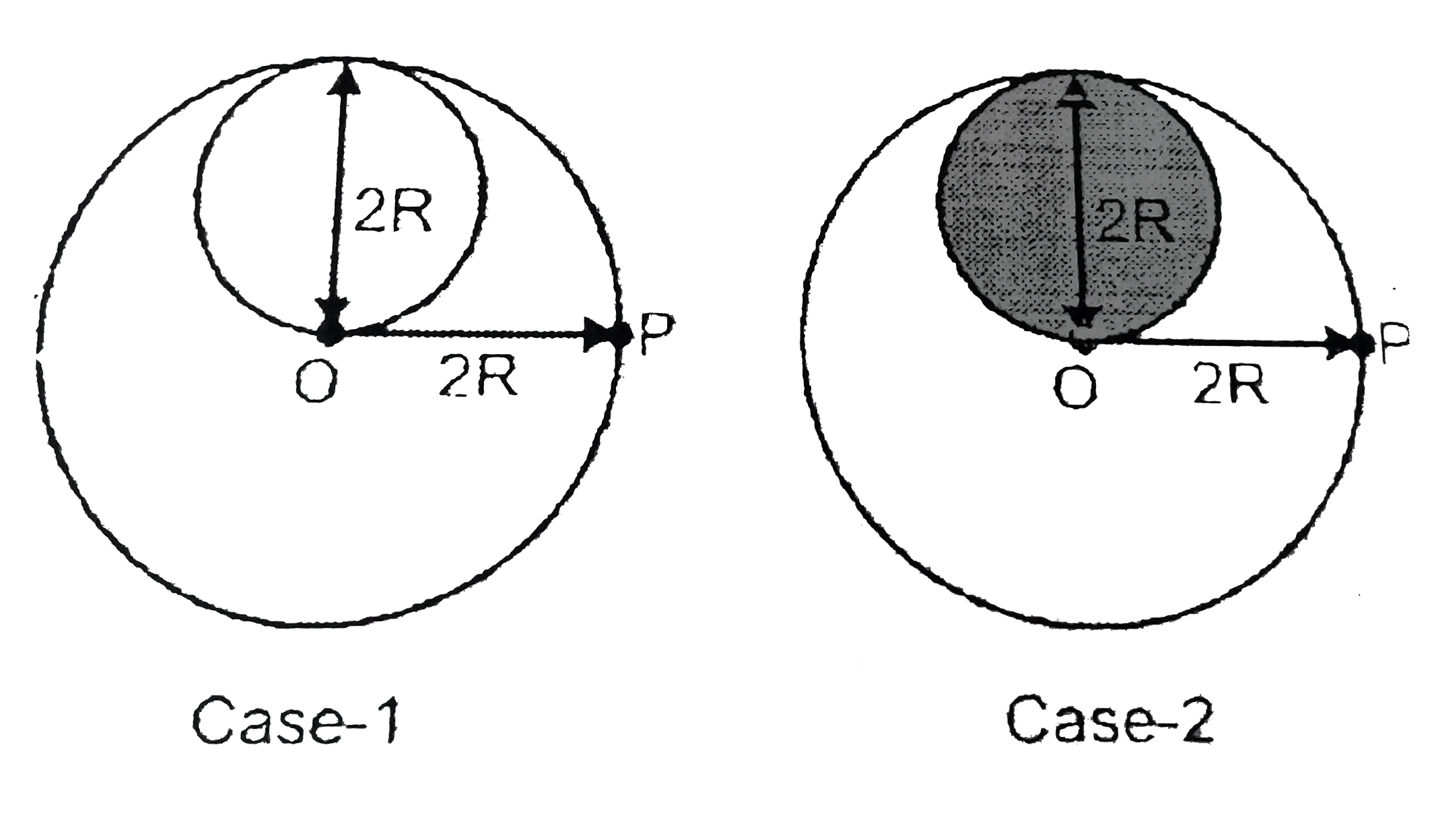
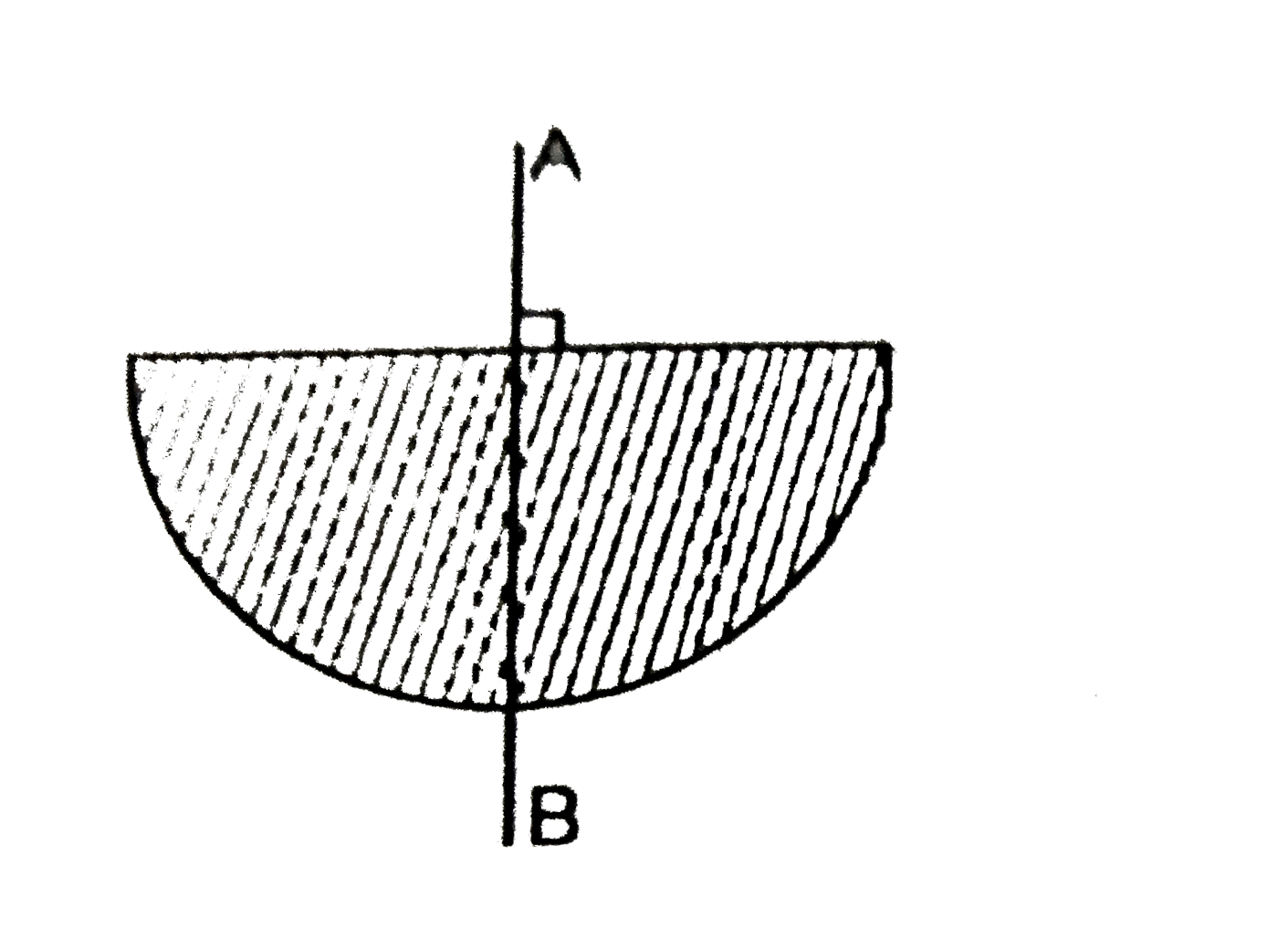
A lamina is made by removing a small disc of diameter 2 R from a bigger disc of uniform mass density and radius 2R, as shown in figure. A second similar disc is made but instead of hole a disc of triple the density as of first it filled in the hole. Centre of mass is calculated in both the cases and was found at a distance r1&r2 from centre O respectively find the ratio ∣∣∣2r2r1∣∣∣View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
 View Solution
View SolutionFrom a disc of mass 2kg and radius 4m a small disc of radius 1 m with center O' is extracted . The new moment of inertia,about an axis passing through O perpendicular to plane of disc is
 View Solution
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 View Solution
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution

