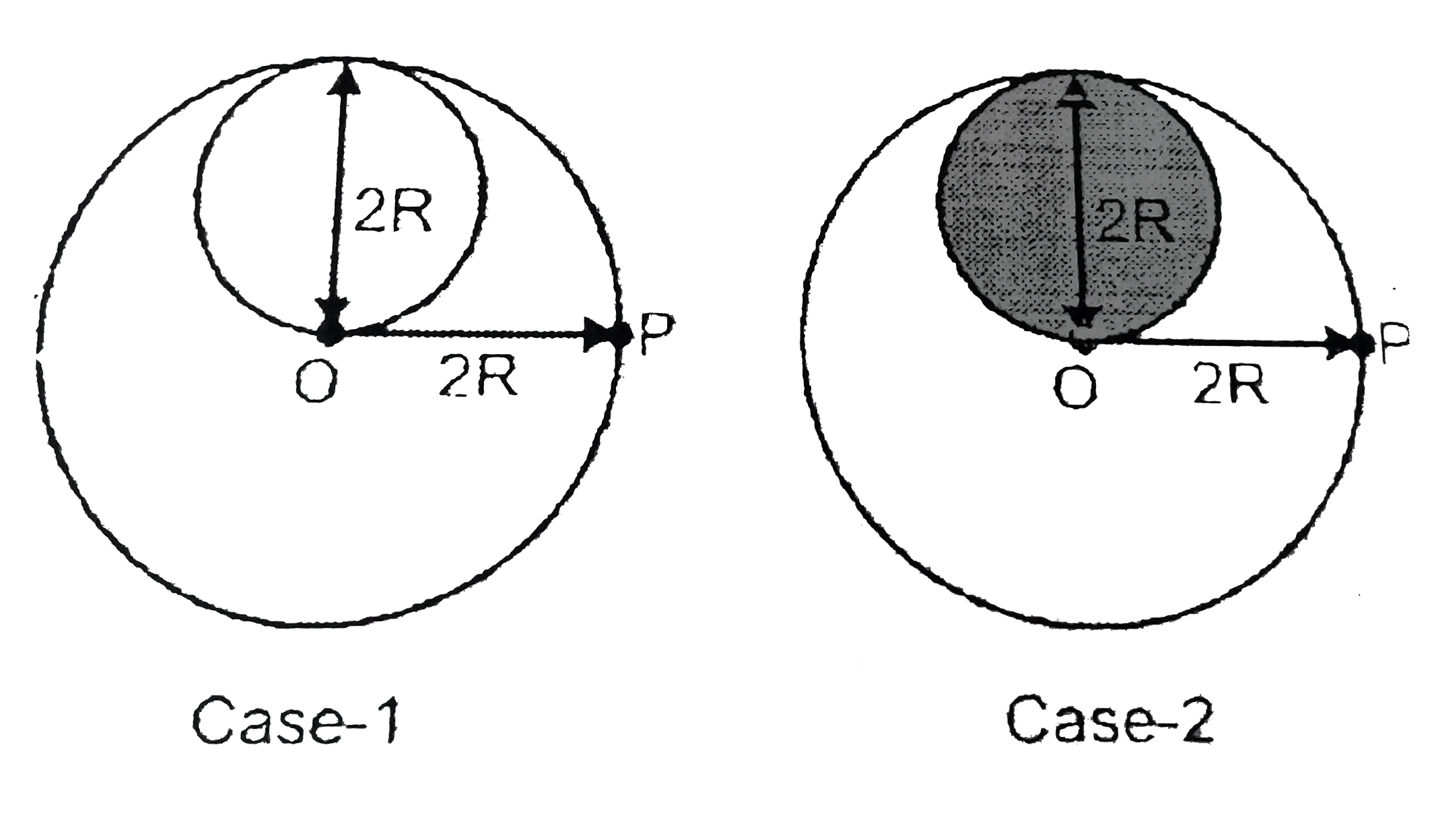
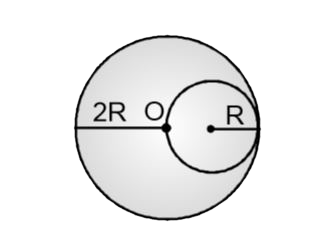
A lamina is made by removing a small disc of diameter 2 R from a bigger disc of uniform mass density and radius 2R, as shown in figure. A second similar disc is made but instead of hole a disc of triple the density as of first it filled in the hole. Centre of mass is calculated in both the cases and was found at a distance r1&r2 from centre O respectively find the ratio ∣∣∣2r2r1∣∣∣
The correct Answer is:2
r1=[−σ×πR2]×R[−σ×πR2]+[σ×π(2R)2]
&r2=[2σ×πR2]×R[2σ×πR2]+[σ×π(2R)2]⇒∣∣∣2r2r1∣∣∣=2
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendiucalr to the plane of the lamina. The ratio IPIO ot the nearest integer is
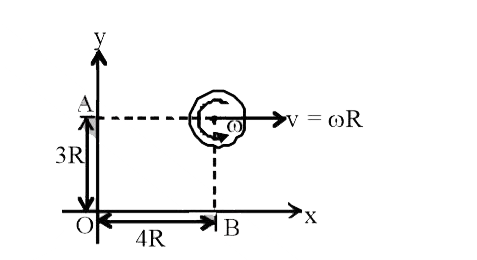
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View Solution
Knowledge Check
A solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
AR3BR2CR6DR4A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
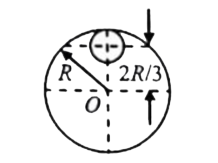 A4MR2B9MR2C379MR2D409MR2
A4MR2B9MR2C379MR2D409MR2A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
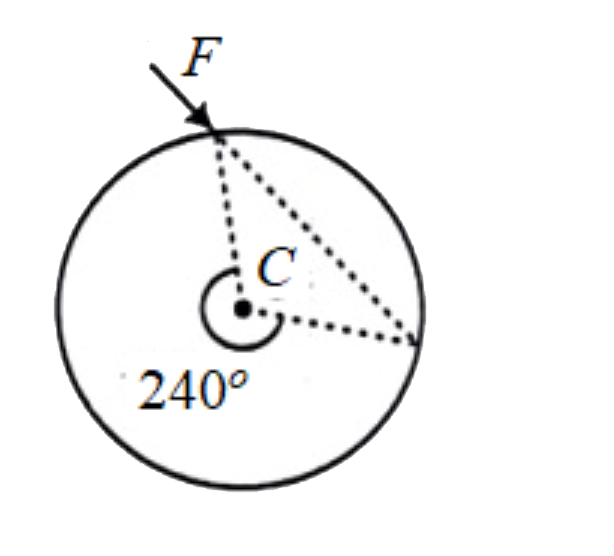 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MR
Two equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA uniform disc having radius 2R and mass density σ as shown in figure. If a small disc of radius R is cut from the disc as shown. Then find out the moment of inertia of remaining disc around the axis that passes through O and is perpendicular to the plane of the page.
View SolutionCalculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View Solution
