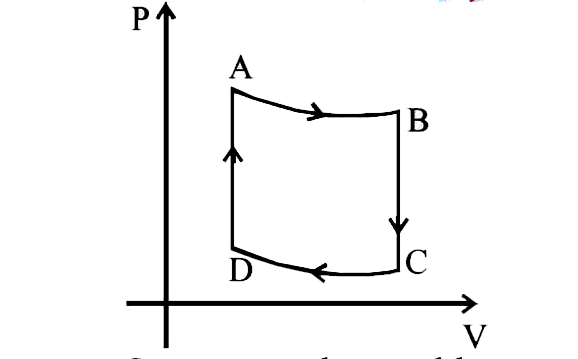
One mole of a monatomic ideal gas is taken through the cycle shown in figure
 The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option.
The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option.
The work done by the gas in the process A→B is 1869.75J
The heat lost by the gas sin the process B→C is -5297.25J
Temperature TD is 500K
Work done from B→C is 40J
The correct Answer is:D
For A→B,TγP1−γ=TγP1−γ
Where γ=5/3 for a monatiomic gas.
TB=TAPB(PA)1−(1)/(γ)=100023)2/5=850K
Work dine in an adiabatic process is given by
W=(nRTA−TBγ−1=1×8.31(1000−850)(5/3)−1)=1869.75J
∴ Process B→C is isochoric
Hence W=0 and PCTCxTB=(1/3)PA2/3PA)TB=TB2=8502=425K
From first law of thermodynamics ,
Q=ΔU+W=nCVΔT+0=n32R(TC−850)
Hence Q=1×32×8.31(125−850)=−5297.625J
Negative sign implies that the system has lost heat.
process D→A is isochoric
PDPA=TDTAorPD=PATDTA
Process C→D is adiabatic
Therefore, TD(TC)γ=PATD(PCTA)γ−1
∴T1/gmma=(C)[PAPCTA]1−1/γ
⇒T3/5=TC[PA(1/3)PA×1000))]2/5=425(31000)2/5
TD=500K
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - MCQs
6 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Carnot Engine
9 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
On mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
<
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure The pressure and temperature at A, B etc are denoted by PA,PB−,TA,TB−, etc respectively
A → B adiabatic expansion
B → C cooling at constant volume
C→D adiabatic compression
D→A heating at constant volume
Given that : TA=1000 K, PB=23PA and PC=13PA
_E01_271_Q01.png)
the heat lost by the gas in process B→C
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure The pressure and temperature at A, B etc are denoted by PA,PB,TA,TB−, etc respectively
A → B adiabatic expansion
B → C cooling at constant volume
C→D adiabatic compression
D→A heating at constant volume
Given that : TA=1000 K, PB=23PA and PC=13PA
_E01_271_Q01.png)
the work done by the gas in process A → B
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume

The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
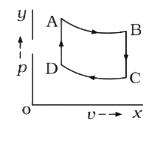
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View Solution
