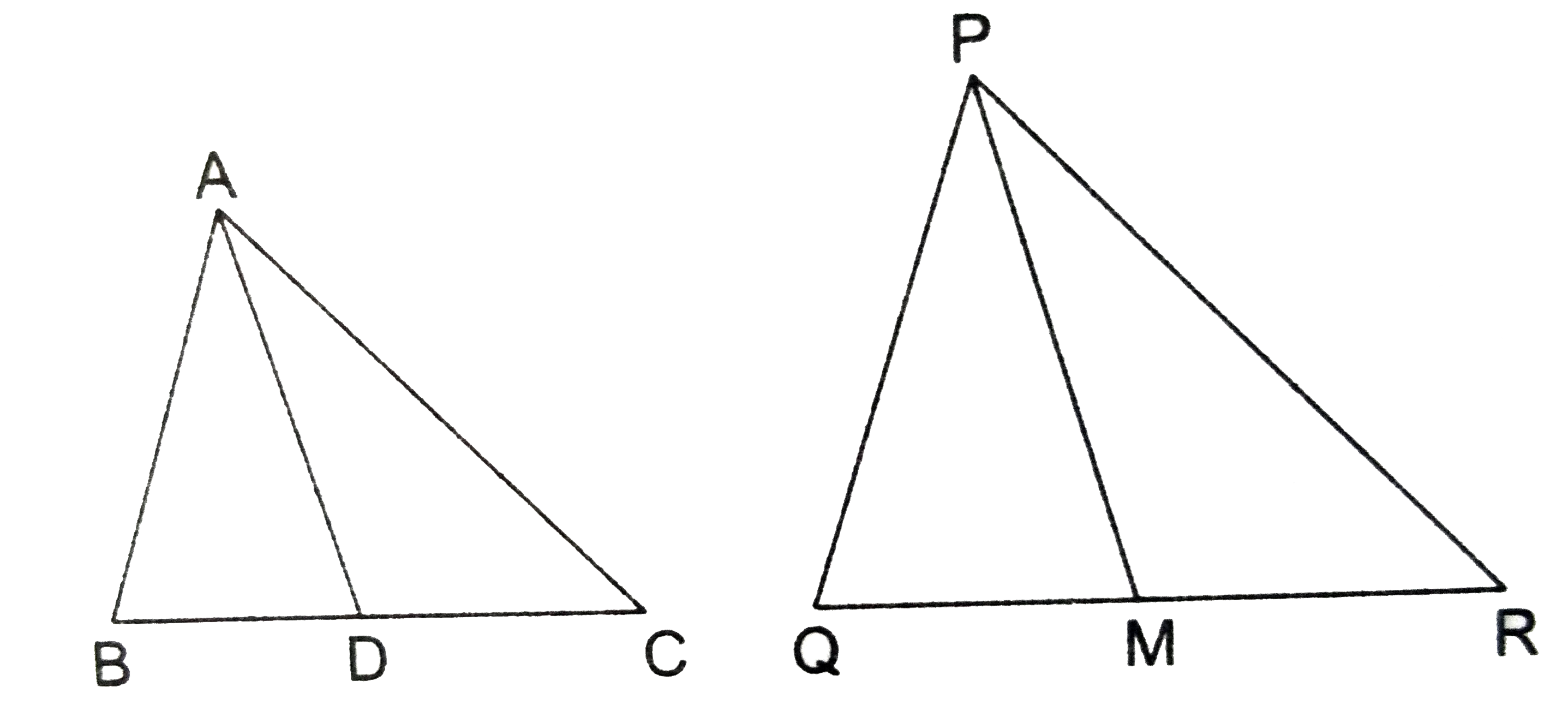
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
To prove that triangle ABC is similar to triangle PQR given that sides AB and AC and median AD of triangle ABC are respectively proportional to sides PQ and PR and median PM of triangle PQR, we can follow these steps:
1. Understand the Given Information:
We are given that:
ABPQ=ACPR=ADPM
This means that the ratios of the sides and medians of the two triangles are equal.
2. Construct the Triangles:
Let’s denote triangle ABC with vertices A, B, and C, and triangle PQR with vertices P, Q, and R. The median AD in triangle ABC bisects side BC at point D, and the median PM in triangle PQR bisects side QR at point M.
3. Extend the Medians:
Extend the median AD to a point R such that AD = DR. Similarly, extend the median PM to a point S such that PM = MS. This gives us two new points R and S.
4. Identify Parallelograms:
By extending the medians, we can observe that quadrilaterals ABRC and PQSR are formed. Since AD and PM are medians, we have:
- BD = DC (since D is the midpoint of BC)
- QM = MR (since M is the midpoint of QR)
This implies that:
- AB = CR (since opposite sides of parallelograms are equal)
- AC = BR
5. Use the Proportionality:
From the given proportionality, we have:
ABPQ=ACPR
This implies that:
ABAC=PQPR
Therefore, we can conclude that the sides of triangle ABC are proportional to the sides of triangle PQR.
6. Angle-Angle (AA) Similarity Criterion:
Since we have established that:
- ABPQ=ACPR
- The angles at A and P (angle BAC and angle QPR) are equal (by construction).
By the Angle-Angle (AA) similarity criterion, we can conclude that:
△ABC∼△PQR
Conclusion:
Thus, we have shown that triangle ABC is similar to triangle PQR.
We are given that:
ABPQ=ACPR=ADPM
This means that the ratios of the sides and medians of the two triangles are equal.
Let’s denote triangle ABC with vertices A, B, and C, and triangle PQR with vertices P, Q, and R. The median AD in triangle ABC bisects side BC at point D, and the median PM in triangle PQR bisects side QR at point M.
Extend the median AD to a point R such that AD = DR. Similarly, extend the median PM to a point S such that PM = MS. This gives us two new points R and S.
By extending the medians, we can observe that quadrilaterals ABRC and PQSR are formed. Since AD and PM are medians, we have:
- BD = DC (since D is the midpoint of BC)
- QM = MR (since M is the midpoint of QR)
- AB = CR (since opposite sides of parallelograms are equal)
- AC = BR
From the given proportionality, we have:
ABPQ=ACPR
This implies that:
ABAC=PQPR
Therefore, we can conclude that the sides of triangle ABC are proportional to the sides of triangle PQR.
Since we have established that:
- ABPQ=ACPR
- The angles at A and P (angle BAC and angle QPR) are equal (by construction).
△ABC∼△PQR
Thus, we have shown that triangle ABC is similar to triangle PQR.
Similar Questions
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
AΔABD≅ΔPQMBΔABC≅ΔPQRCΔABD≅ΔPMRDΔADC≅ΔPMR
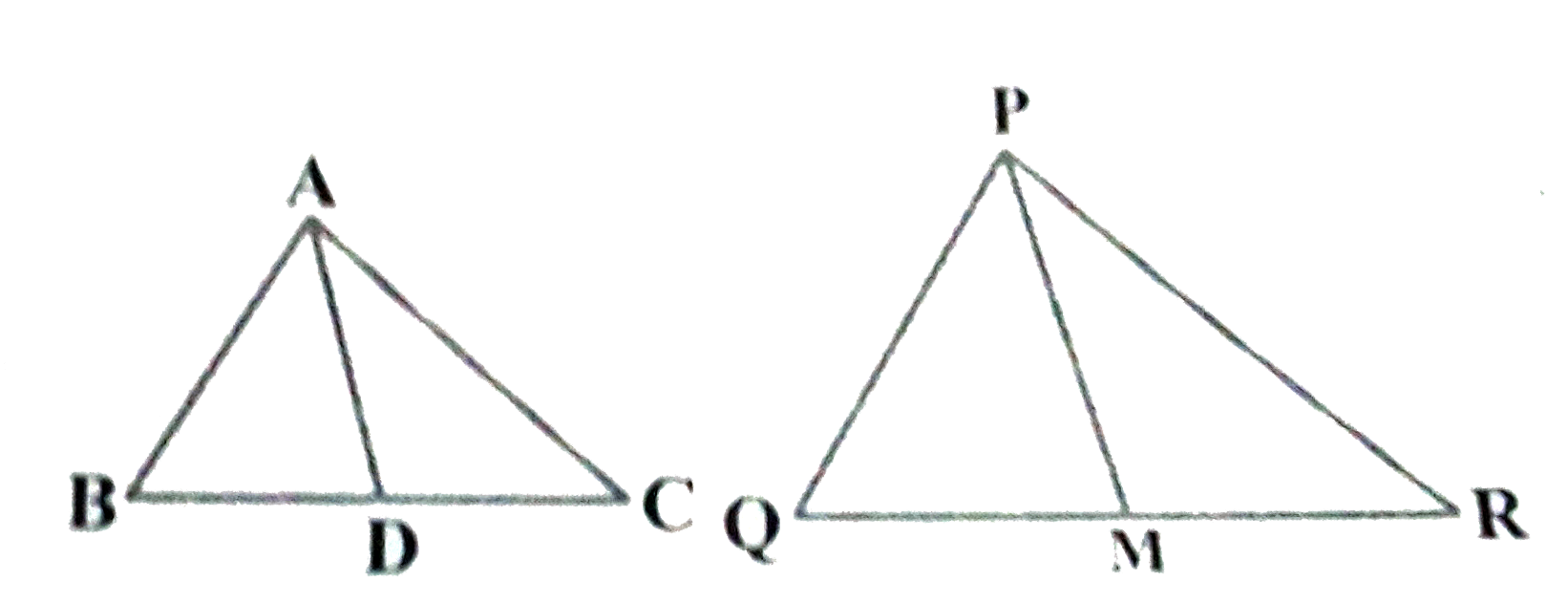
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
 View Solution
View SolutionSides AB and BC and median AD of a triangle ABC are respectively propor-/ tional to sides PQ and QR and median PM of ΔPQR (see Fig. 6.41). Show that ΔABC~ΔPOR.
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
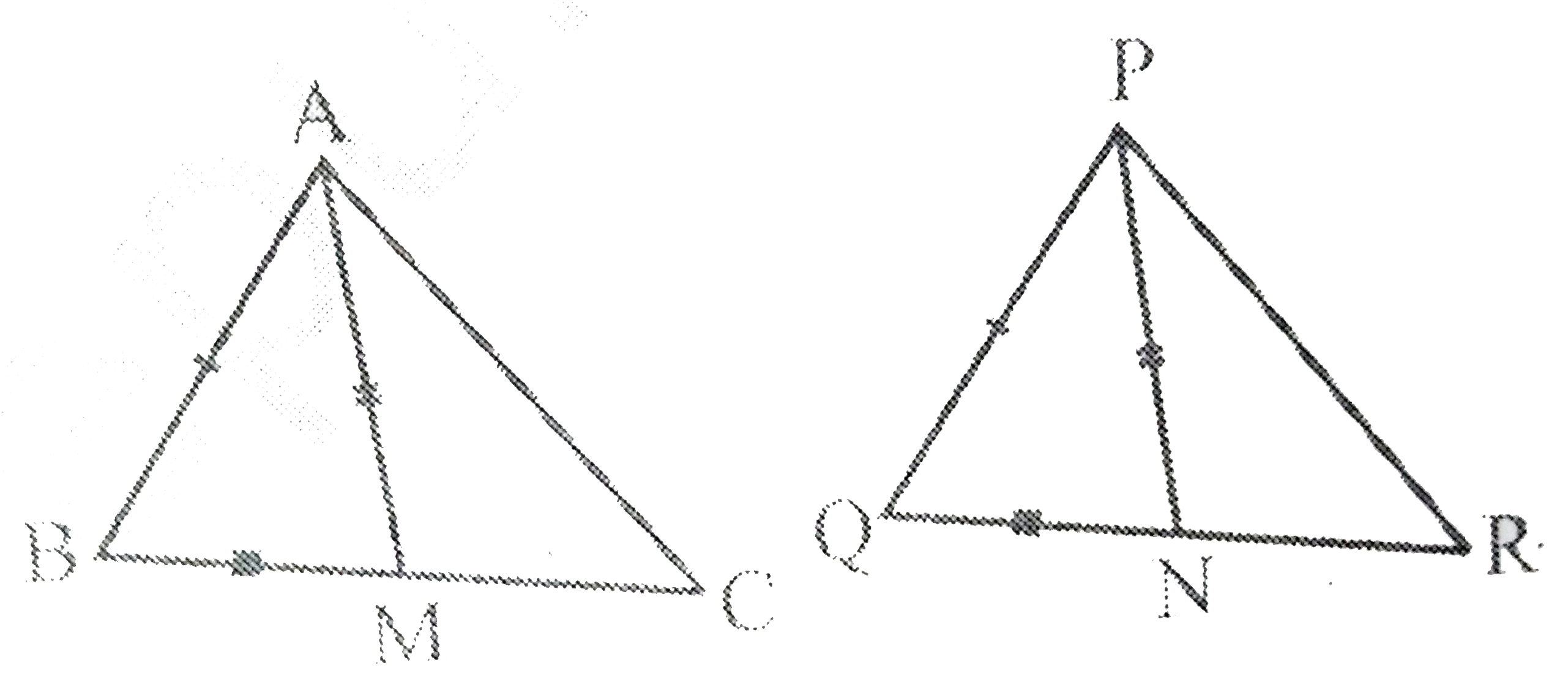
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that

ΔABM≅ΔPQNView SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
 View Solution
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIf two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and corresponding median of another triangle; then triangle are similar.
View Solution

