A wheel of radius 2 m rolls on the ground with uniform velocity 4ms−1. . The relative acceleration of the topmost point of the wheel with respect to the bottom - most point of the wheel is
8ms−2
16ms−2
4ms−2
32ms−2
The correct Answer is:B
To solve the problem of finding the relative acceleration of the topmost point (Q) of a rolling wheel with respect to the bottommost point (P), we can follow these steps:
Step 1: Understand the motion of the wheel
The wheel is rolling with a uniform velocity of V=4m/s and has a radius R=2m.
Step 2: Calculate the angular velocity (ω)
Using the relationship between linear velocity and angular velocity:
ω=VR
Substituting the values:
ω=4m/s2m=2rad/s
Step 3: Determine the accelerations at points P and Q
- The bottommost point (P) of the wheel is in contact with the ground and has zero acceleration in the vertical direction because it is not moving.
- The topmost point (Q) of the wheel is moving in a circular path and experiences centripetal acceleration.
Step 4: Calculate the centripetal acceleration at point Q
The centripetal acceleration (ac) is given by:
ac=ω2R
Substituting the values:
ac=(2rad/s)2×2m=4×2=8m/s2
Step 5: Calculate the total acceleration of point Q
The total acceleration of point Q consists of the centripetal acceleration directed towards the center of the wheel and the tangential acceleration, which is zero since the wheel rolls with uniform velocity. Therefore, the total acceleration of Q is:
aQ=ac=8m/s2
Step 6: Determine the relative acceleration of Q with respect to P
Since point P has zero acceleration, the relative acceleration of Q with respect to P is simply the acceleration of Q:
aQ/P=aQ−aP=8m/s2−0=8m/s2
Final Answer
The relative acceleration of the topmost point of the wheel with respect to the bottommost point of the wheel is:
8m/s2
The wheel is rolling with a uniform velocity of V=4m/s and has a radius R=2m.
Using the relationship between linear velocity and angular velocity:
ω=VR
Substituting the values:
ω=4m/s2m=2rad/s
- The bottommost point (P) of the wheel is in contact with the ground and has zero acceleration in the vertical direction because it is not moving.
- The topmost point (Q) of the wheel is moving in a circular path and experiences centripetal acceleration.
The centripetal acceleration (ac) is given by:
ac=ω2R
Substituting the values:
ac=(2rad/s)2×2m=4×2=8m/s2
The total acceleration of point Q consists of the centripetal acceleration directed towards the center of the wheel and the tangential acceleration, which is zero since the wheel rolls with uniform velocity. Therefore, the total acceleration of Q is:
aQ=ac=8m/s2
Since point P has zero acceleration, the relative acceleration of Q with respect to P is simply the acceleration of Q:
aQ/P=aQ−aP=8m/s2−0=8m/s2
The relative acceleration of the topmost point of the wheel with respect to the bottommost point of the wheel is:
8m/s2
Topper's Solved these Questions
Similar Questions
A wheel of radius R=1 m rolls on ground with uniform velocity v=2 m/s . Calculate the relative acceleration of topmost point of wheel with respect to bottom most point (in m/s2).
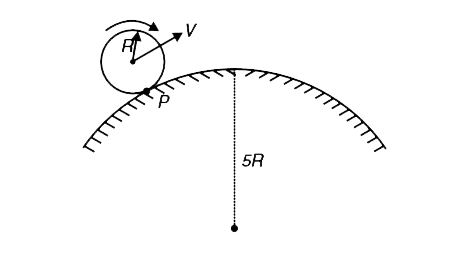
View SolutionA convex surface has a uniform radius of curvature equal to 5R. A wheel of radius R is rolling without sliding on it with a constant speed v. Find the acceleration of the point (P) of the wheel which is in contact with the convex surface.
View Solution
Knowledge Check
A wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
Av2RB2v2RCv22RD4v2RA wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is
AvB2vCv/2DzeroA wheel of radius R rolls on the ground with a unifrom velocity v. The velocity of topmost point releative to bottom must point is
AzeroB2υCυDυ/2
A wheel of radius r rolling on a straight line, the velocity of its centre being v. At a certain instant the point of contact of the wheel the ground is M and N is the highest point on the wheel (diametricaly opposite to M). The incorrect statement is -
View SolutionIf acycle wheel of radius 0.4 m completes one revolution in one second , then the acceleration of a point on the rim is in one second , then the acceleration of a point on the rim is
View SolutionA wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
View SolutionIf a cycle wheel of radius 4 m completes one revolution in two seconds. Then acceleration of a point on the cycle wheel will be
View SolutionA cycle wheel of radius 0.4 m completes one revolution in one second then the acceleration of a point on the cycle wheel will be
View Solution