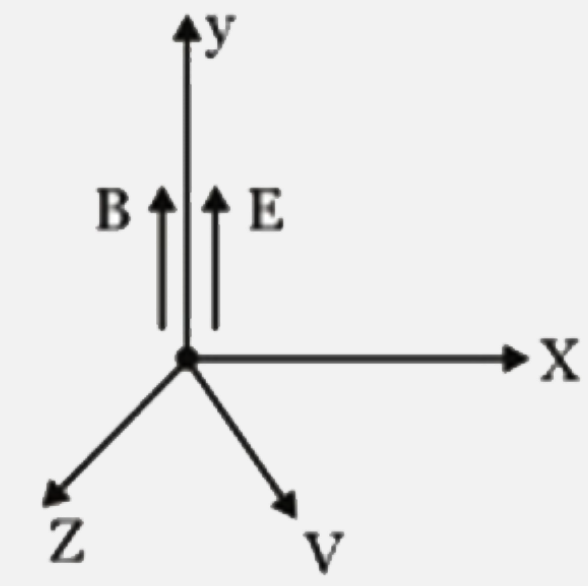
A positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
√v2+qE2my
√(BE)2+v2+qE2my
√v2+2qEmy
None of the above
The correct Answer is:C
Step by step video & image solution for A positive charge particle having change q and mass m has velocity vecv = v((hati+hatk)/sqrt2) in the magnetic field B at the origin . Its speed as the function of y is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A charged particle of mass 5mg and charge q=+2μC has velocity →v=2ˆi−3ˆj+4ˆk. Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field →B=3ˆj−2ˆk,→v and →B are in m/s and Wb/m2 respectively.
View SolutionA particle having charge q=10μC and mass m = 3 mg has a velocity →v = (10 cm) (ˆi+2ˆj) at t =0 at origin. There exists a uniform magnetic field →B=0.6πTˆi. Another uncharged particle is moving with a constant velocity along negative x-axis. At t =0 its x coordinate is +50 cm. The two particles collide and stick together and the combined mass goes in a circular path. Find the possible values of the mass of the uncharged particle .
View Solution
Knowledge Check
A charged particle of charge Q and massm moves with velocity v in a circular path due to transverse magnetic field, B, then its frequency is
AQB2πmBQvB2πmCQmvB2πDvb2πQmA particle of charge q and mass m, is fired perpenducular to a magnetic field (B) with a velocity v. What is the frequency of revolution of the particle?
A2πBqB2πBqmC2πmBqDBq2πmA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
Amv0qBB2mv0qBCmv02qBDNone of these
A uniform magnetic field →B is set up along the positive x-axis. A particle of charge q and mass m moving with a velocity →v enters the field at the origin in X - Y plane such that it has velocity components both along and perpendicular to the magnetic field →B. Trace, giving reasons, the trajectory followed by the particle. Find out the expression for the distance moved by the particle along the magnetic field in one rotation.
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
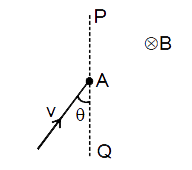
impulse of magnetic force.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
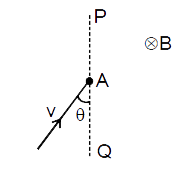
time spent
View Solution
