The following fusion reaction take place 221A→32B+n+3.27 MeV. If 2 kg of .21A is subjected to the above reaction, the energy released is used to light a 100 W light a lamp, how long will the lamp glow ?
7×103 years
3×105 years
5×104 years
2×106 years
The correct Answer is:C
To solve the problem step by step, we will follow these instructions:
Step 1: Calculate the number of moles of 21A
Given that the mass of 21A is 2 kg, we first convert this to grams:
Mass=2kg=2000g
The molecular mass of 21A is 2 g/mol.
Now, we can calculate the number of moles (n):
n=massmolecular mass=2000g2g/mol=1000mol
Step 2: Calculate the number of atoms
Using Avogadro's number (NA=6.022×1023atoms/mol), we can find the total number of atoms:
Number of atoms=n×NA=1000mol×6.022×1023atoms/mol=6.022×1026atoms
Step 3: Calculate the total energy released
From the reaction, we know that 2 atoms of 21A release 3.27 MeV of energy. Therefore, the energy released per atom is:
Energy per atom=3.27MeV2=1.635MeV
To convert MeV to joules, we use the conversion factor 1MeV=1.6×10−13J:
Energy per atom in joules=1.635MeV×1.6×10−13J/MeV=2.616×10−13J
Now, the total energy released by all atoms is:
Total energy=Number of atoms×Energy per atom=6.022×1026×2.616×10−13J≈1.577×1014J
Step 4: Calculate the time the lamp will glow
The power of the lamp is given as 100 W. The time (t) for which the lamp will glow can be calculated using the formula:
t=Total energyPower=1.577×1014J100W=1.577×1012s
Step 5: Convert seconds to years
To convert seconds to years, we use the conversion factor 1year≈3.154×107s:
t(in years)=1.577×1012s3.154×107s/year≈5.00×104years
Final Answer
The lamp will glow for approximately 5.00×104 years.
---
Given that the mass of 21A is 2 kg, we first convert this to grams:
Mass=2kg=2000g
The molecular mass of 21A is 2 g/mol.
n=massmolecular mass=2000g2g/mol=1000mol
Using Avogadro's number (NA=6.022×1023atoms/mol), we can find the total number of atoms:
Number of atoms=n×NA=1000mol×6.022×1023atoms/mol=6.022×1026atoms
From the reaction, we know that 2 atoms of 21A release 3.27 MeV of energy. Therefore, the energy released per atom is:
Energy per atom=3.27MeV2=1.635MeV
To convert MeV to joules, we use the conversion factor 1MeV=1.6×10−13J:
Energy per atom in joules=1.635MeV×1.6×10−13J/MeV=2.616×10−13J
Now, the total energy released by all atoms is:
Total energy=Number of atoms×Energy per atom=6.022×1026×2.616×10−13J≈1.577×1014J
The power of the lamp is given as 100 W. The time (t) for which the lamp will glow can be calculated using the formula:
t=Total energyPower=1.577×1014J100W=1.577×1012s
To convert seconds to years, we use the conversion factor 1year≈3.154×107s:
t(in years)=1.577×1012s3.154×107s/year≈5.00×104years
The lamp will glow for approximately 5.00×104 years.
Topper's Solved these Questions
Similar Questions
Following reaction takes place in one step: 2NO+O2+2NO2 How will the rate of above reaction change if the volume of reaction vessel is reduced to 1/3 rd of original volume? Will there be any change in the order of reaction?
View SolutionCalculate the energy released in the following reaction
.3Li6+.0n1→.2He4+.1H3
View Solution
Knowledge Check
Which of the following reactions take place by SN2 reaction?
A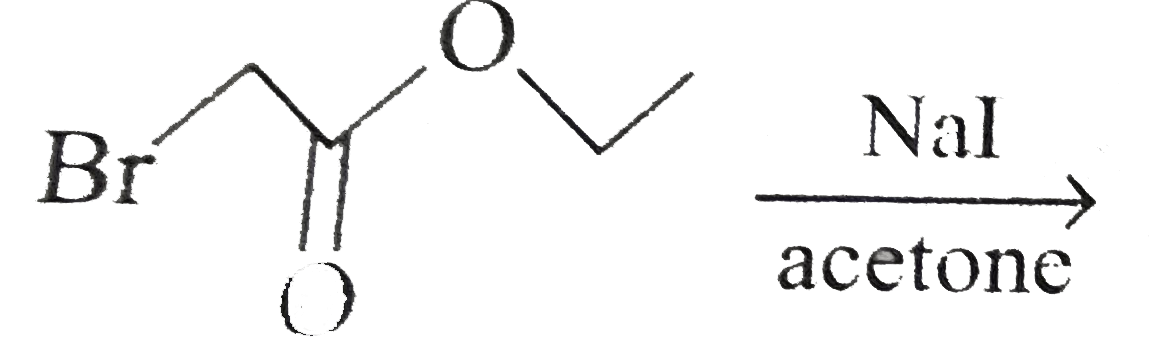 B
B C
C D
D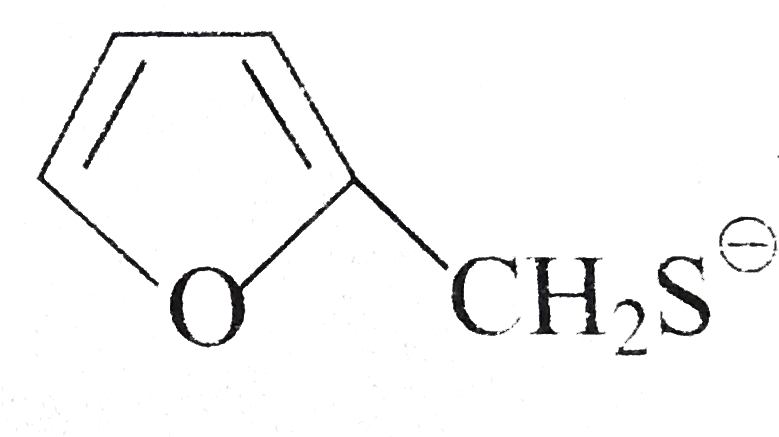
if in a nuclear fusion reaction, mass defect to 0.3% , then energy released in fusion of 1 kg mass
A27×1010 JB27×1011 JC27×1012 JD27×1013 JFor a reaction, 12A→2B rate of disappearance of A is related to the rate of appearance of B by the expression
A−d[A]dt=4d[B]dtB=d[A]dt=12d[B]dtC−d[A]dt=14d[B]dtD−d[A]dt=d[B]dt
In the fusion reaction _12H+21H→32He+10n, the masses of deuteron, helium and neutron expressed in amu are 2.015, 3.017 and 1.009 respectively. If 1 kg of deuterium undergoes complete fusion, find the amount of total energy released. 1 amu =931.5MeV/c2.
View SolutionA nuclear fusion reaction is given by
.1H2+.1H2→.1He3+.10n+Q(energy).
If 2 moles of deuterium are fused, then total released energy is
View SolutionIn the reaction 3A→2B, rate of reaction +d[B]dt is equal to :
View SolutionIn the reaction .21H+.31H→.42He+.10n, if the binding energies of .21H,.31H and .42He are respectively a,b and c (in MeV), then the energy (in MeV) released in this reaction is.
View SolutionRead the following statement and the conclisions that follow. Decide which of the two conclusions follow from the given statements
Statements :
• Some bulbs are lights
• All lightes are lamps
Conclusions :
1. Some bulbs are lamps.
2. No light is a bulb.
View Solution
