A current of 2.34 A flows in resistance of 11.111111Ω The potential difference across the given resistance with due regard for the significant figure is
26.000 A
26.00 A
26.0 V
26 V
The correct Answer is:C
To solve the problem of finding the potential difference across a resistance when a current flows through it, we will use Ohm's Law, which states:
V=I×R
Where:
- V is the potential difference (voltage),
- I is the current (in amperes),
- R is the resistance (in ohms).
1. Identify the Given Values:
- Current I=2.34A
- Resistance R=11.111111Ω
2. Apply Ohm's Law:
- Substitute the values into the formula:
V=I×R=2.34A×11.111111Ω
3. Perform the Multiplication:
- Calculate the product:
V=2.34×11.111111=25.99999994V
4. Round to the Correct Number of Significant Figures:
- The current 2.34 has three significant figures.
- The resistance 11.111111 has eight significant figures.
- The result should be rounded to three significant figures (the lesser number of significant figures).
- Thus, 25.99999994 rounded to three significant figures is 26.0V.
5. Final Answer:
- The potential difference across the resistance is:
V=26.0V
- V is the potential difference (voltage),
- I is the current (in amperes),
- R is the resistance (in ohms).
- Current I=2.34A
- Resistance R=11.111111Ω
- Substitute the values into the formula:
V=I×R=2.34A×11.111111Ω
- Calculate the product:
V=2.34×11.111111=25.99999994V
- The current 2.34 has three significant figures.
- The resistance 11.111111 has eight significant figures.
- The result should be rounded to three significant figures (the lesser number of significant figures).
- Thus, 25.99999994 rounded to three significant figures is 26.0V.
- The potential difference across the resistance is:
V=26.0V
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the above question, potential difference across the 40Ω resistance will be
AZeroB80VC40VD120VA current ofImAis flowing through a resistance of 1000Ω. To measure the potential difference across it, a voltmeter should be used whose resistance is
A1000ΩB100ΩCvery large as compared to 103ΩDzeroΩIn the given circuit diagram, potential difference across 2Ω resistance is
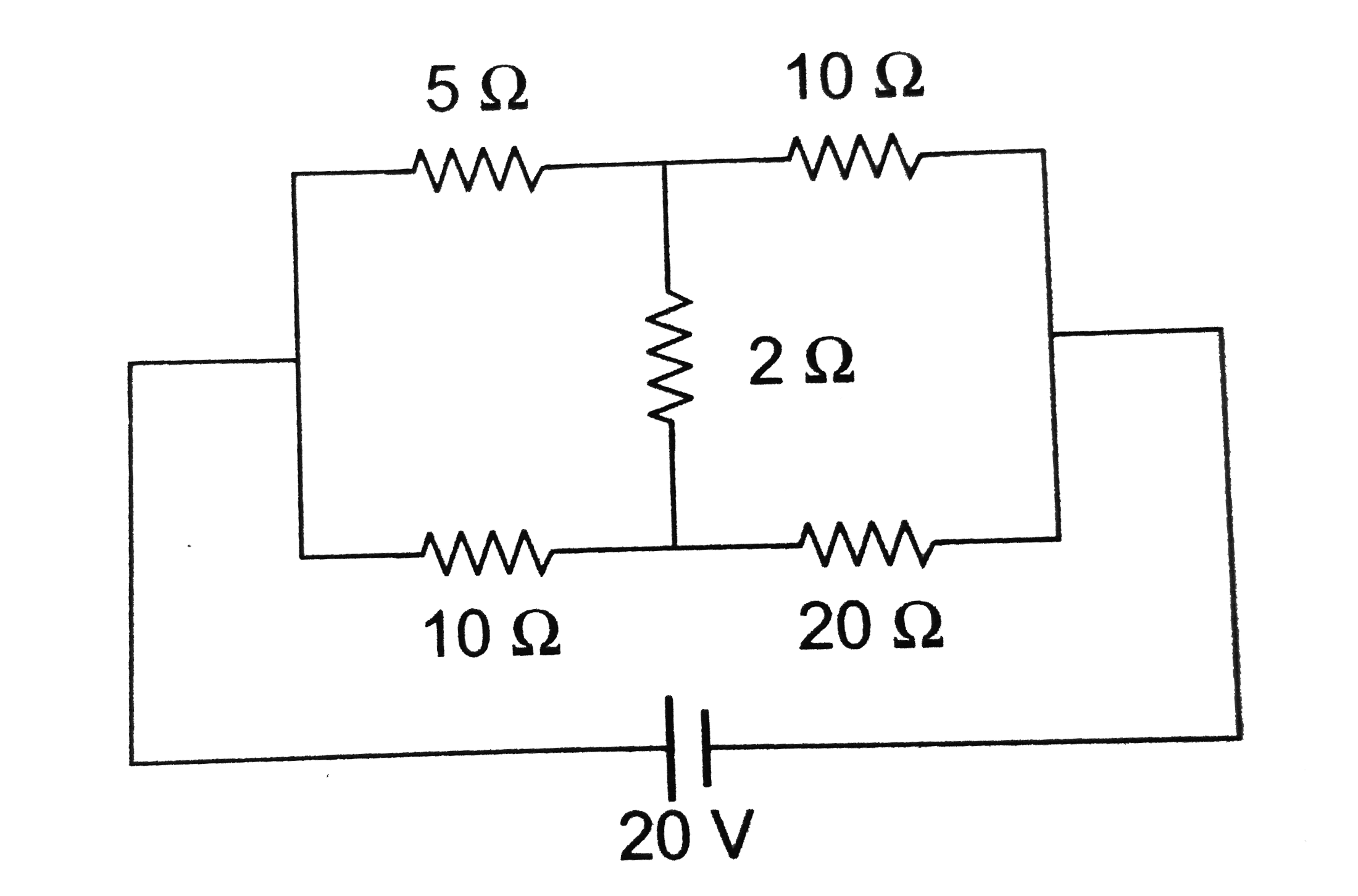 A4VB6VC20VDzero
A4VB6VC20VDzero
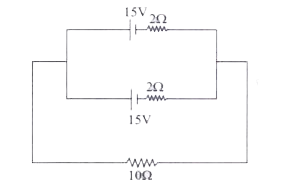
In the given circuit find potential difference across 10ohm resistance
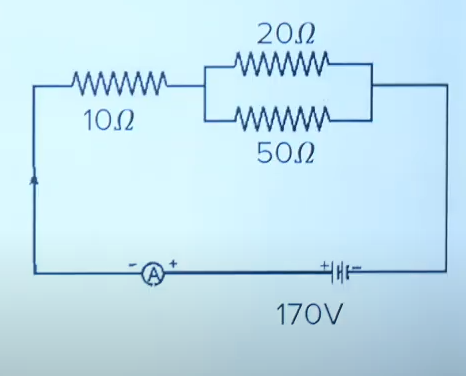
View SolutionA current of 0.2A flows through a conductor of resistance 4.5Ω. Calculate the potential difference at the ends of the conductor.
View SolutionIf a current of 3 A flows through a wire of resistance 8 ohms, calculate the potential difference applied across its ends.
View SolutionFor the circuit shown in the figure what is the potential difference across the external resistance ?
View SolutionA 2-A current flows through a resistor when a potential difference of 20 V is applied across it. The resistance of the resistor is
View Solution