The minimum value of effective capacitance that can be obtained by combining 3 capacitors of capacitances 1 pF, 2pF and 4pF is
47 pF
1 pF
2 pF
74 pE
The correct Answer is:A
To find the minimum value of effective capacitance that can be obtained by combining three capacitors of capacitances 1 pF, 2 pF, and 4 pF, we need to connect them in series. The formula for the equivalent capacitance Ceq of capacitors in series is given by:
1Ceq=1C1+1C2+1C3
Where C1=1pF, C2=2pF, and C3=4pF.
Step 1: Write down the formula for capacitors in series
1Ceq=1C1+1C2+1C3
Step 2: Substitute the values of the capacitors
1Ceq=11pF+12pF+14pF
Step 3: Calculate each term
Calculating each term gives:
11pF=1
12pF=0.5
14pF=0.25
Step 4: Sum the terms
Now, add these values together:
1Ceq=1+0.5+0.25=1.75
Step 5: Take the reciprocal to find Ceq
Now, take the reciprocal to find Ceq:
Ceq=11.75pF
Step 6: Simplify the fraction
To simplify 11.75:
Ceq=174=47pF
Final Answer
Thus, the minimum value of effective capacitance that can be obtained by combining the three capacitors is:
Ceq=47pF
1Ceq=1C1+1C2+1C3
1Ceq=11pF+12pF+14pF
Calculating each term gives:
11pF=1
12pF=0.5
14pF=0.25
Now, add these values together:
1Ceq=1+0.5+0.25=1.75
Now, take the reciprocal to find Ceq:
Ceq=11.75pF
To simplify 11.75:
Ceq=174=47pF
Thus, the minimum value of effective capacitance that can be obtained by combining the three capacitors is:
Ceq=47pF
Topper's Solved these Questions
Similar Questions
How many different values of capacitances can be obtained with the three given capacitors of capacitances 1μF,3μFand5μF? Use all the capacitors while forming any combination.
View SolutionIf three capacitors of values 1μ F,2μ Fand3μF are available.The maximum and minimum values of capacitances one can obtain by different combinations of the three capacitors together are respectively ???
View Solution
Knowledge Check
The equivalent capacitance of the combination of the capacitors is :
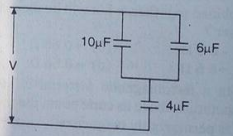 A3.20μFB7.80μFC3.90μFD2.16μF
A3.20μFB7.80μFC3.90μFD2.16μFThe equivalent capacitance of the combination of the capacitors is :
 A3.20μFB7.80μFC3.90μFD2.16μF
A3.20μFB7.80μFC3.90μFD2.16μFWhat is the total capacitance if three capacitors of capacitance 2 pF, 3 pF and 4 pF are connected in parallel?
A9pFB1213pFC1312pFD294pF
The minimum number of capacitors (each of capacitance 2 μ F ) required to get an effective capacitance of 9 μ F is?
View SolutionObtain an expression for the capacitance of a combination of three capacitors in parallel .
View SolutionSeveral 10pF capacitors are given, each capable of withstanding 100V. How would you construct :
(a) a unit possessing a capacitance of 2pF and capable of withstanding 500V?
(b) a unit possessing a capacitance of 20pF and capable of withstanding 300V?
View SolutionElectrostatic energy stored in a capacitor of 12 pF capacitance connected to a 50 V battery is:
View SolutionEffective capacitance of 1011 is required to obtain from such capacitors, each of 2μF find the suitable combination:
View Solution
