How many different values of capacitances can be obtained with the three given capacitors of capacitances 1μF,3μFand5μF? Use all the capacitors while forming any combination.
To find out how many different values of capacitance can be obtained using three capacitors with capacitances of 1μF, 3μF, and 5μF, we will analyze the combinations of these capacitors in both series and parallel arrangements.
1. Capacitance in Parallel:
When capacitors are connected in parallel, the total capacitance Cp is the sum of the individual capacitances:
Cp=C1+C2+C3
For our capacitors:
Cp=1μF+3μF+5μF=9μF
2. Capacitance in Series:
When capacitors are connected in series, the total capacitance Cs is given by the reciprocal of the sum of the reciprocals of the individual capacitances:
1Cs=1C1+1C2+1C3
For our capacitors:
1Cs=11μF+13μF+15μF
Calculating this gives:
1Cs=1+13+15=1+0.333+0.2=1.533
Therefore,
Cs=11.533≈0.652μF
3. Combination of Two in Parallel and One in Series:
- Case 1: 1μF and 3μF in parallel, and 5μF in series:
Cp1=1μF+3μF=4μF
Ctotal1=14μF+15μF=14+15=5+420=920
Thus,
Ctotal1≈2.22μF
- Case 2: 1μF and 5μF in parallel, and 3μF in series:
Cp2=1μF+5μF=6μF
Ctotal2=16μF+13μF=16+13=1+26=36=12
Thus,
Ctotal2=2μF
- Case 3: 3μF and 5μF in parallel, and 1μF in series:
Cp3=3μF+5μF=8μF
Ctotal3=18μF+11μF=18+1=1+88=98
Thus,
Ctotal3≈1.125μF
4. Combination of Two in Series and One in Parallel:
- Case 1: 1μF and 3μF in series, and 5μF in parallel:
Cs1=11μF+13μF=1+0.3331=1.333
Thus,
Ctotal4=1.333μF+5μF=6.333μF
- Case 2: 1μF and 5μF in series, and 3μF in parallel:
Cs2=11μF+15μF=1+0.21=1.2
Thus,
Ctotal5=1.2μF+3μF=4.2μF
- Case 3: 3μF and 5μF in series, and 1μF in parallel:
Cs3=13μF+15μF=1+0.61=1.6
Thus,
Ctotal6=1.6μF+1μF=2.6μF
Summary of Different Capacitance Values:
- 0.652μF
- 2.22μF
- 2μF
- 1.125μF
- 6.333μF
- 4.2μF
- 2.6μF
- 9μF
Conclusion:
The different values of capacitance that can be obtained using the three capacitors 1μF, 3μF, and 5μF are:
- 0.652μF
- 1.125μF
- 2μF
- 2.22μF
- 2.6μF
- 4.2μF
- 6.333μF
- 9μF
Thus, there are 8 different values of capacitance that can be obtained.
When capacitors are connected in parallel, the total capacitance Cp is the sum of the individual capacitances:
Cp=C1+C2+C3
For our capacitors:
Cp=1μF+3μF+5μF=9μF
When capacitors are connected in series, the total capacitance Cs is given by the reciprocal of the sum of the reciprocals of the individual capacitances:
1Cs=1C1+1C2+1C3
For our capacitors:
1Cs=11μF+13μF+15μF
Calculating this gives:
1Cs=1+13+15=1+0.333+0.2=1.533
Therefore,
Cs=11.533≈0.652μF
- Case 1: 1μF and 3μF in parallel, and 5μF in series:
Cp1=1μF+3μF=4μF
Ctotal1=14μF+15μF=14+15=5+420=920
Thus,
Ctotal1≈2.22μF
Cp2=1μF+5μF=6μF
Ctotal2=16μF+13μF=16+13=1+26=36=12
Thus,
Ctotal2=2μF
Cp3=3μF+5μF=8μF
Ctotal3=18μF+11μF=18+1=1+88=98
Thus,
Ctotal3≈1.125μF
- Case 1: 1μF and 3μF in series, and 5μF in parallel:
Cs1=11μF+13μF=1+0.3331=1.333
Thus,
Ctotal4=1.333μF+5μF=6.333μF
Cs2=11μF+15μF=1+0.21=1.2
Thus,
Ctotal5=1.2μF+3μF=4.2μF
Cs3=13μF+15μF=1+0.61=1.6
Thus,
Ctotal6=1.6μF+1μF=2.6μF
- 0.652μF
- 2.22μF
- 2μF
- 1.125μF
- 6.333μF
- 4.2μF
- 2.6μF
- 9μF
The different values of capacitance that can be obtained using the three capacitors 1μF, 3μF, and 5μF are:
- 0.652μF
- 1.125μF
- 2μF
- 2.22μF
- 2.6μF
- 4.2μF
- 6.333μF
- 9μF
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Tough & Tricky PROBLEMS10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)11videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 518videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of spherical capacitor when capacitance is 1 μF is:
A1.11mB9kmC10mD1.11cm - Question 2 - Select One
The radius of spherical capacitor when capacitance is 1μF is:
A1⋅11mB9 kmC10 mD1⋅11cm - Question 3 - Select One
In the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
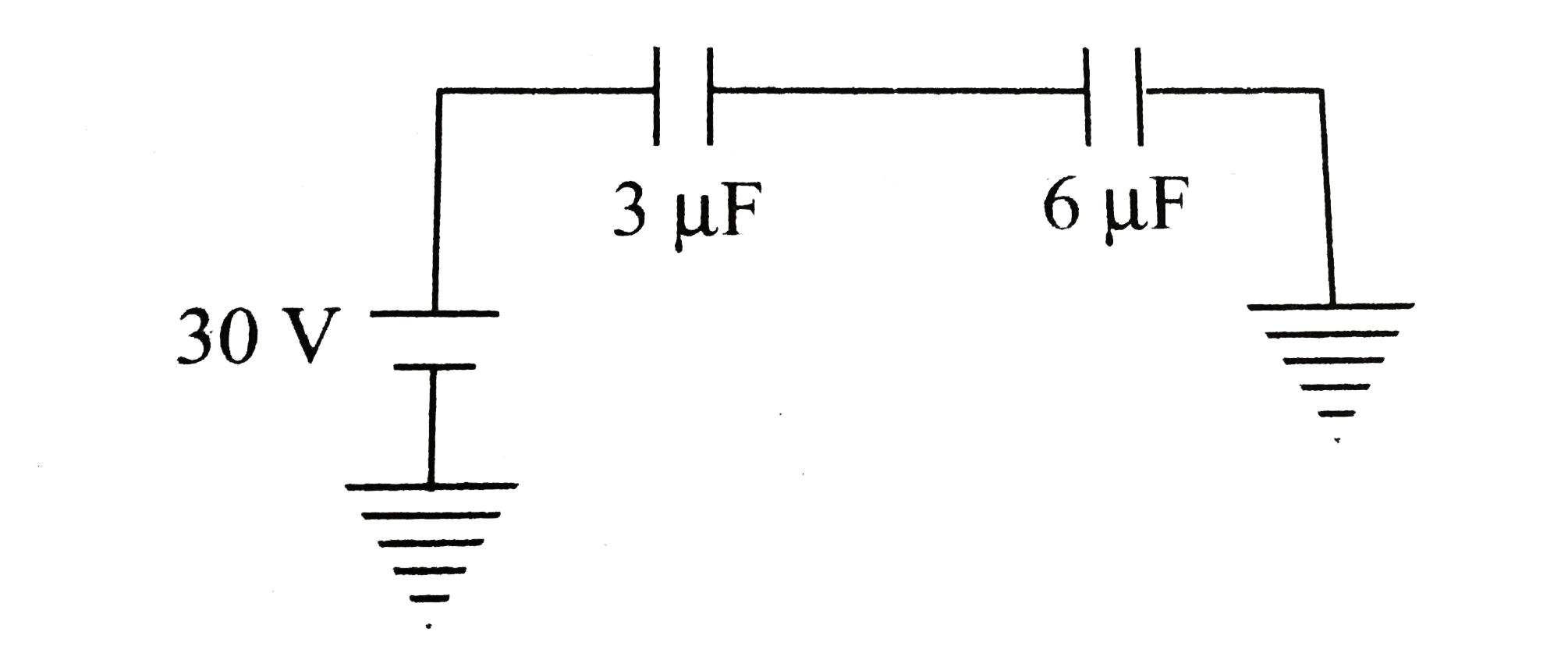 AzeroB40μCC60μCD90μC
AzeroB40μCC60μCD90μC
Theee capacitors of capacitance 1,2,and 3 μF connected in series. Find the resultant capacitance.
View SolutionFind equivalent capacitance between A and B in the combination givenbelow. Each capacitor is of 2μF capacitance.
View SolutionFind equivalent capacitance between A and B in the combination given below. Each capacitor is of 2μF capacitance.
 View Solution
View SolutionConnect three capacitors of 3μF,3μF and 6μF such that their equivalent capacitance is 5μF.
View SolutionA 200 V battery is connected across the combination of capacitors of capacities 5μFand10μF in series. The charge on each capacitor is
View Solution