In the relation $\frac{d y}{d t} = 2 ω sin (ω t + ϕ_{0})$ , the dimensional formula for $ω t + ϕ_{0}$ is

$[M L T]$

$[M L T^{0}]$

$[M L^{0} T 0]$

$[M^{0} L^{0} T^{0}]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Answer

Step by step video, text & image solution for In the relation ( dy)/( dt) = 2 omega sin ( omega t + phi_(0)), the dimensional formula for omega t + phi_(0) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

In the relation $y = r sin (ω t - k x)$ , the dimensions of $ω / k$ are
A $[M^{0} L^{0} T^{0}]$
B $[M^{0} L^{1} T^{- 1}]$
C $[M^{0} L^{0} T^{1}]$
D $[M^{0} L^{1} T^{0}]$
If $i_{1} = i_{0} sin (ω t), i_{2} = i_{0_{2}} sin (ω t + ϕ)$ , then $i_{3} =$

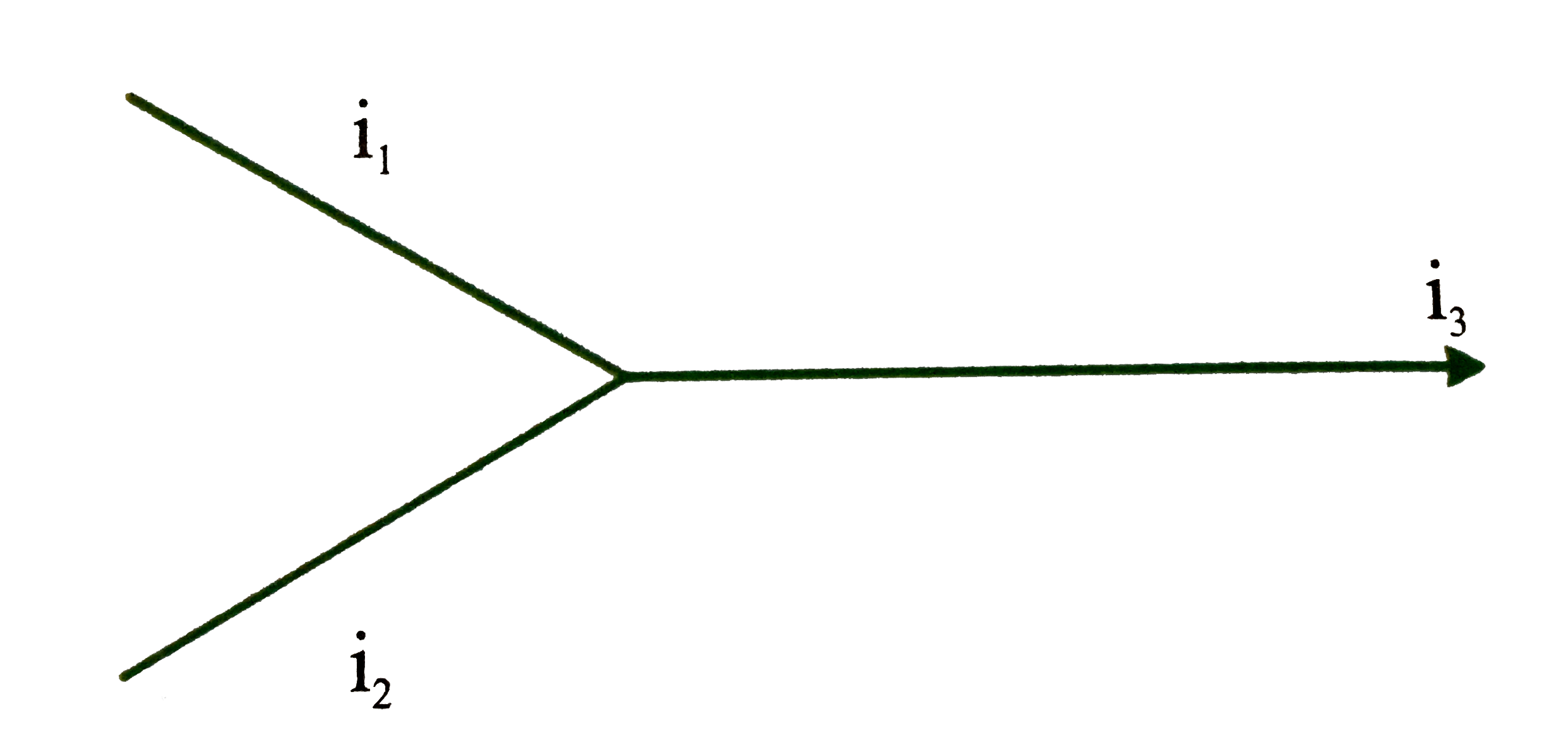A $\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2}} sin {ϕ + ω t}$
B $(i_{0_{1}} + i_{0_{2}}) sin (\frac{ϕ}{2} + ω t)$
C $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [ϕ + ω t]$
D $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [α + ω t]$ where $α = {Tan}^{- 1} [\frac{i_{0_{2}} sin ϕ}{i_{0_{1}} + i_{0_{2}} cos ϕ}]$
What are the dimensional formulae of $ω$ and K in the relation $y = A sin (ω t - K x)$ ?
A $[M^{0} L^{0} T^{2}] [M^{0} L^{- 1} T^{0}]$
B $[M^{0} L^{0} T^{- 1}] [M^{0} L^{- 1} T^{0}]$
C $[M^{0} L^{0} T^{- 1}] [M^{0} L^{1} T^{0}]$
D $[M^{0} L^{0} T^{- 1}] [M^{0} L^{1} T^{- 1}]$