A small object of mass of 100 g moves in a circular path . At a given instant velocity of the object is 10ˆims−1 and acceleration is (20ˆi+10ˆj)ms−2. At this instant of time. the rate of change of kinetic energy of the object is
200kg m2s−2
300kg m2s−2
10000kg m2s−2
20kg m2s−2
The correct Answer is:D
To find the rate of change of kinetic energy of the object, we can follow these steps:
Step 1: Understand the Kinetic Energy Formula
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
Step 2: Differentiate Kinetic Energy with Respect to Time
To find the rate of change of kinetic energy, we differentiate KE with respect to time t:
d(KE)dt=ddt(12mv2)=12md(v2)dt
Using the chain rule, we can express d(v2)dt as:
d(v2)dt=2v⋅dvdt
Thus, we have:
d(KE)dt=12m⋅2v⋅dvdt=mv⋅dvdt
Step 3: Substitute the Values
Given:
- Mass m=100g=0.1kg
- Velocity v=10^im/s
- Acceleration a=20^i+10^jm/s2
We need to find dvdt, which is equal to the acceleration a.
Step 4: Calculate the Rate of Change of Kinetic Energy
Substituting the values into the formula:
d(KE)dt=mv⋅a
Calculating v⋅a:
v⋅a=(10^i)⋅(20^i+10^j)=10⋅20+0=200m2/s2
Now substituting m=0.1kg:
d(KE)dt=0.1⋅200=20W
Final Answer
The rate of change of kinetic energy of the object is:
d(KE)dt=20W
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
To find the rate of change of kinetic energy, we differentiate KE with respect to time t:
d(KE)dt=ddt(12mv2)=12md(v2)dt
Using the chain rule, we can express d(v2)dt as:
d(v2)dt=2v⋅dvdt
Thus, we have:
d(KE)dt=12m⋅2v⋅dvdt=mv⋅dvdt
Given:
- Mass m=100g=0.1kg
- Velocity v=10^im/s
- Acceleration a=20^i+10^jm/s2
Substituting the values into the formula:
d(KE)dt=mv⋅a
Calculating v⋅a:
v⋅a=(10^i)⋅(20^i+10^j)=10⋅20+0=200m2/s2
Now substituting m=0.1kg:
d(KE)dt=0.1⋅200=20W
The rate of change of kinetic energy of the object is:
d(KE)dt=20W
Topper's Solved these Questions
Similar Questions
A small object of mass of 100 g moves in a circular path. At a given instant velocity of the object is 10ˆim/s and acceleration is (20ˆi+10ˆj)m/s2. At this instant of time, rate of change of kinetic energy (in kg m2s−3) of the object is
View SolutionAn object of mass 1 kg is moving with a velocity 10 m/s. Find the kinetic energy of the object
View Solution
Knowledge Check
An object of 10 kg is moving with a speed of 2 m/s. The kinetic energy of the object is:
A20 JB5 JC10 JD40 JAn object of 10 kg is moving with a speed of 2 m/s. The kinetic energy of the object is:
A20 JB5JC10 JD40 JA particle is moving on a circular path of 10 m radius. At any instant of time, its speed is 5ms−1 and the speed is increasing at a rate of 2ms−2. At this instant, the magnitude of the net acceleration will be
A3.2ms−2B2ms−2C1.2ms−2D4.3ms−2
A particle is moving in an isolated x−y plane. At an instant, the particle has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2. At that instant what will be the radius of curvature of its path ?
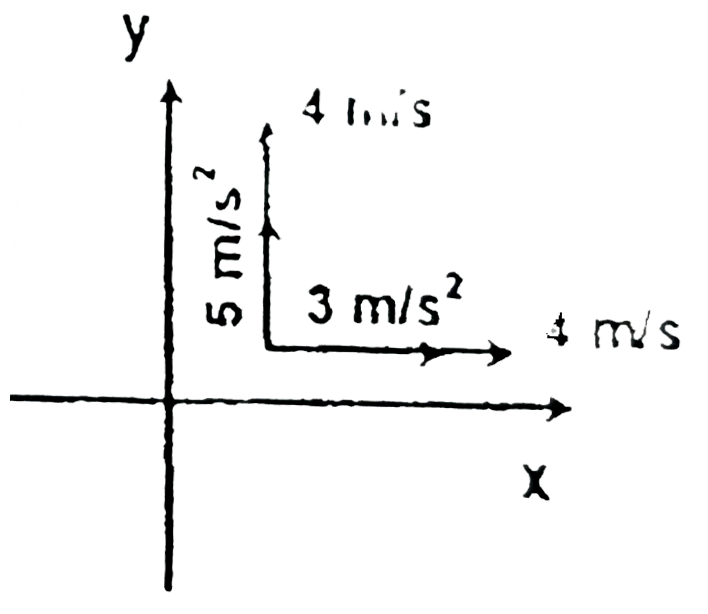
View SolutionAn object of 1kg mass has a momentum of 10 kg m / sec then the kinetic energy of the object will be
View SolutionA particle is moving in such a way that at one instant velocity vector of the particle is 3ˆi+4ˆjm/s and acceleration vector is −25ˆi−25ˆjm/s? The radius of curvature of the trajectory of the particle at that instant is
View SolutionA car of mass m moves in a horizontal circular path of radius r metre. At an instant its speed is Vm/s and is increasing at a rate of am/sec2.then the acceleration of the car is
View SolutionA 120 g mass has a velocity →v=2ˆi+5ˆjms−1 at a certain instant. Its kinetic energy is
View Solution
