Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities . When points A and C are maintained at different temperature, no heat flows through the central rod if
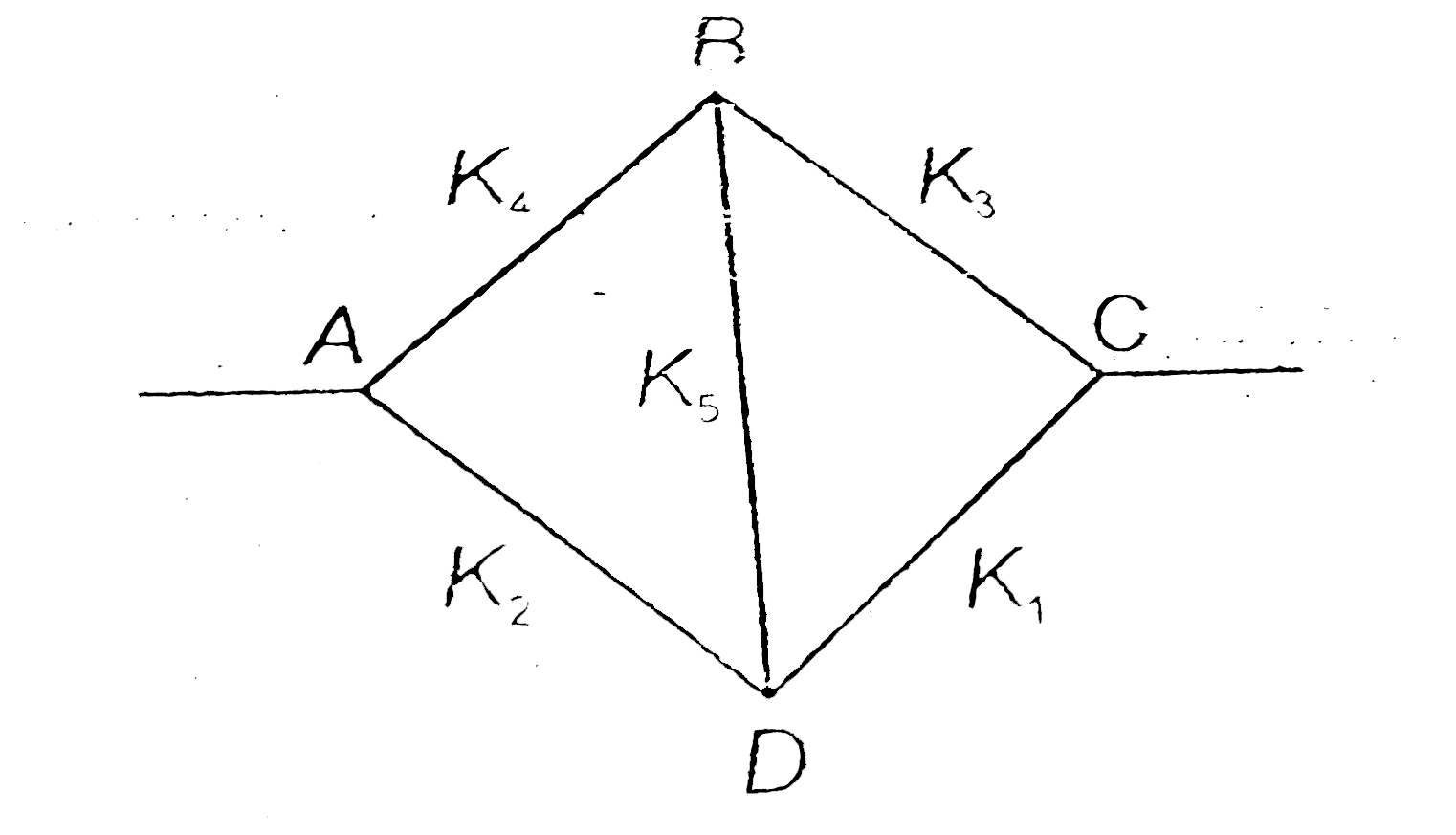
The correct Answer is:A
Step by step video, text & image solution for Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities k_(1),k_(2),k_(3) and k_(5). When points A and C are maintained at different temperature, no heat flows through the central rod if by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K

View SolutionA composite body consists of two rectangular plates of the same dimensions but different thermal conductivities KAandKB . This body is used to transfer heat between two objects maintained at different temperatures. The composite body can be placed such that flow of heat takes place either parallel to the interface or perpendicular to it. Calculate the effective thermal conductivities K∣∣andK⊥ of the composite body for the parallel and perpendicular orientations. Which orientation will have more thermal conductivity ?
View Solution
Knowledge Check
Five rods of same dimensions are arrranged as shown in the figure. They have thermal conductivities K1,K2,K3,K4 and K5. When points A and B are maintained at different themperature, no heat flows through the central rod if
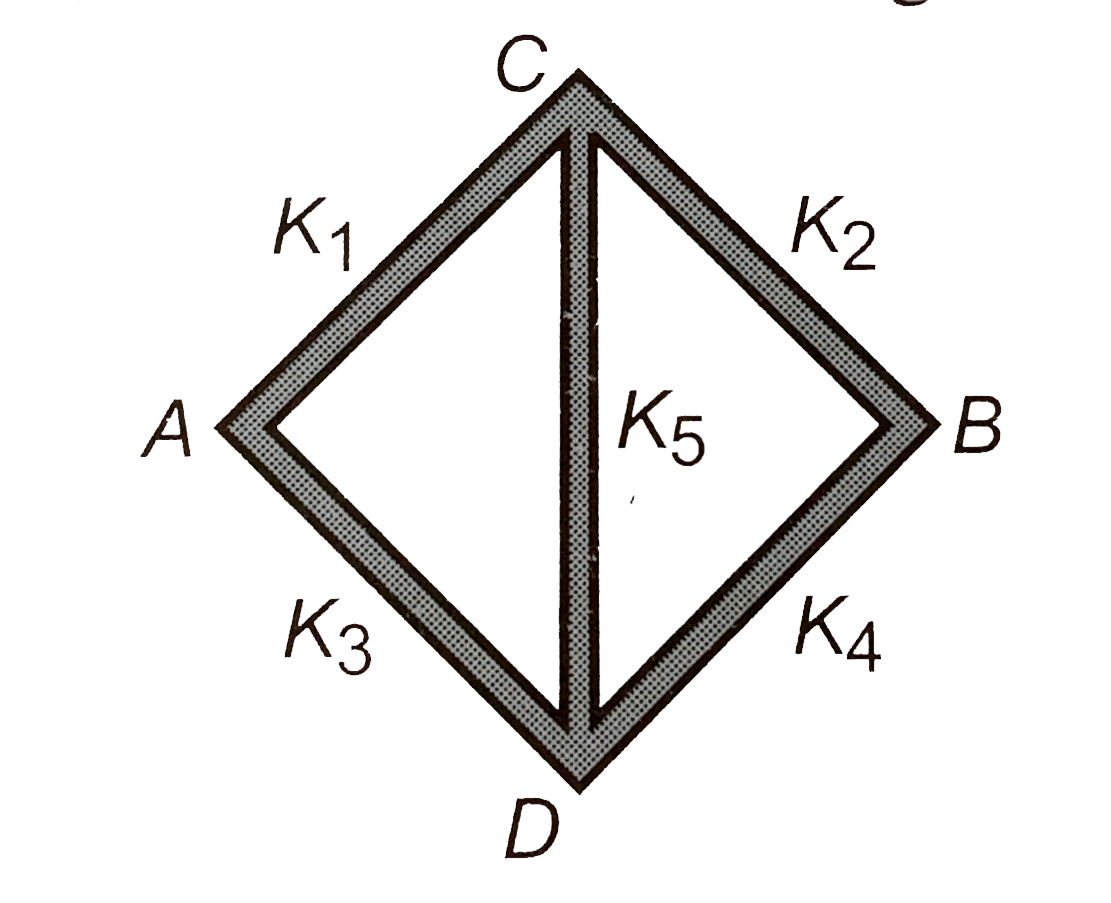 AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3
AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities K1,K2,K3,K4 and K5 . When points A and B are maintained at different temperatures, no heat flows through the central rod if
 AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3
AK1=K4 and K2=K3BK1K4=K2K3CK1K2=K3K4DK1K4=K2K3
Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities K1,K2 and K3. The points P and Q are maintained at different temeperature for the heat to flow at the same rate along PRQ and PQ. Whi of the following options correct?AK3=12(K1+K2)BK3=K1+K2CK3=K1K2K1+K2DK3=2(K1+K2)
Three rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionRate of heat flow through two conducting rods of identiclal dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionA cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
View Solution
