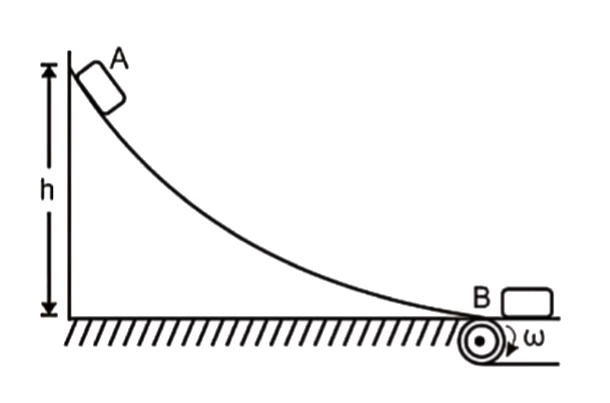
Particles are released from rest A and side down the smooth surface of hight h to a conveyor B. The correct angular veleocity ω of the coneyor pulley of readius r to prevent any siding on the beit as the particles transfer to the conveyou is

√2gh
2ghr
√2ghr
2gh2r2
The correct Answer is:C
Step by step video, text & image solution for Particles are released from rest A and side down the smooth surface of hight h to a conveyor B. The correct angular veleocity omega of the coneyor pulley of readius r to prevent any siding on the beit as the particles transfer to the conveyou is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A block A starts sliding on a smooth track from a height h as shown in the figure. The track smoothly joins into a conveyor belt which is being driven by a pulley of radius r. I the angular velocity ω of the pulley is such that the block A doesn't slip on the belt, the value of ω is
 View Solution
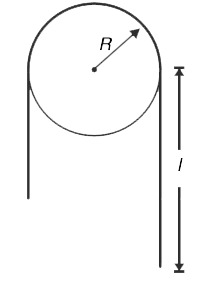
View SolutionA rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Particles are released from rest A and slide down the smooth surface of hight h to a conveyor B. The correct angular veleocity ω of the coneyor pulley of radius r to prevent any sliding on the belt as the particles transfer to the conveyor is
 A√2ghB2ghrC√2ghrD2gh2r2
A√2ghB2ghrC√2ghrD2gh2r2 - Question 2 - Select One or More
A particle of mass m is released from a height H on a smooth curved surface which ends into a vertical loop of radius R, as shown. Choose the correct alernative(s) if H=2R.
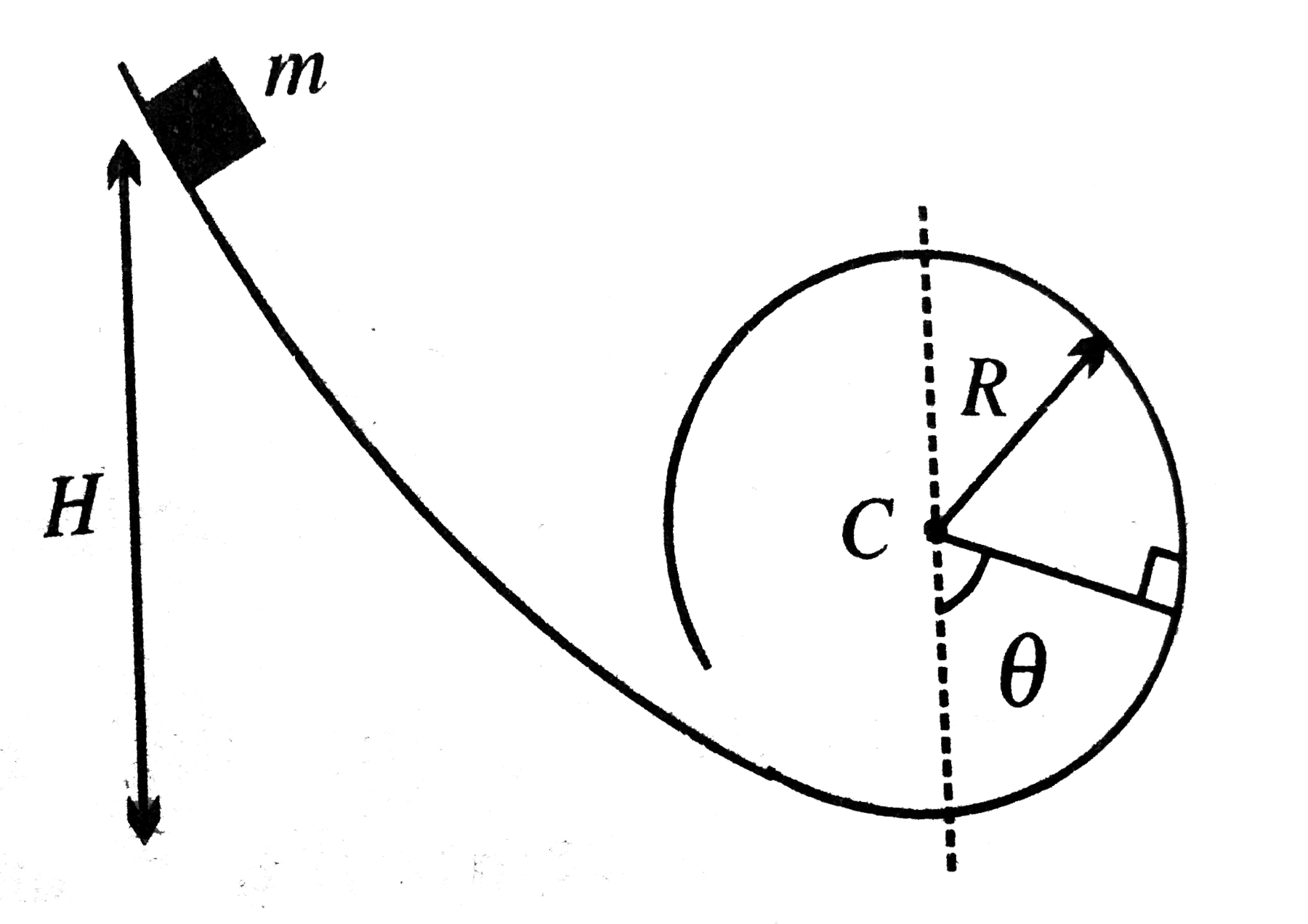 AThe particles reaches the top of the loop with zero velocityBThe particle cannot reach the top of the loop.CThe particle breaks off at a height h=R from the base of the loop.DThe particle breaks off at a height h from the base of the loop such that R<h<2R
AThe particles reaches the top of the loop with zero velocityBThe particle cannot reach the top of the loop.CThe particle breaks off at a height h=R from the base of the loop.DThe particle breaks off at a height h from the base of the loop such that R<h<2R - Question 3 - Select One
A particle of mass m oscillates inside the smooth surface a fixed pipe of radius R. The axis of the pipe is horizontal and the particle moves from B to A and back. At an instant the kinetic energy of the particle is K (say at position of the particle shown in figure ). Then choose the correct value of force applied by particle on the pipe at this instant.
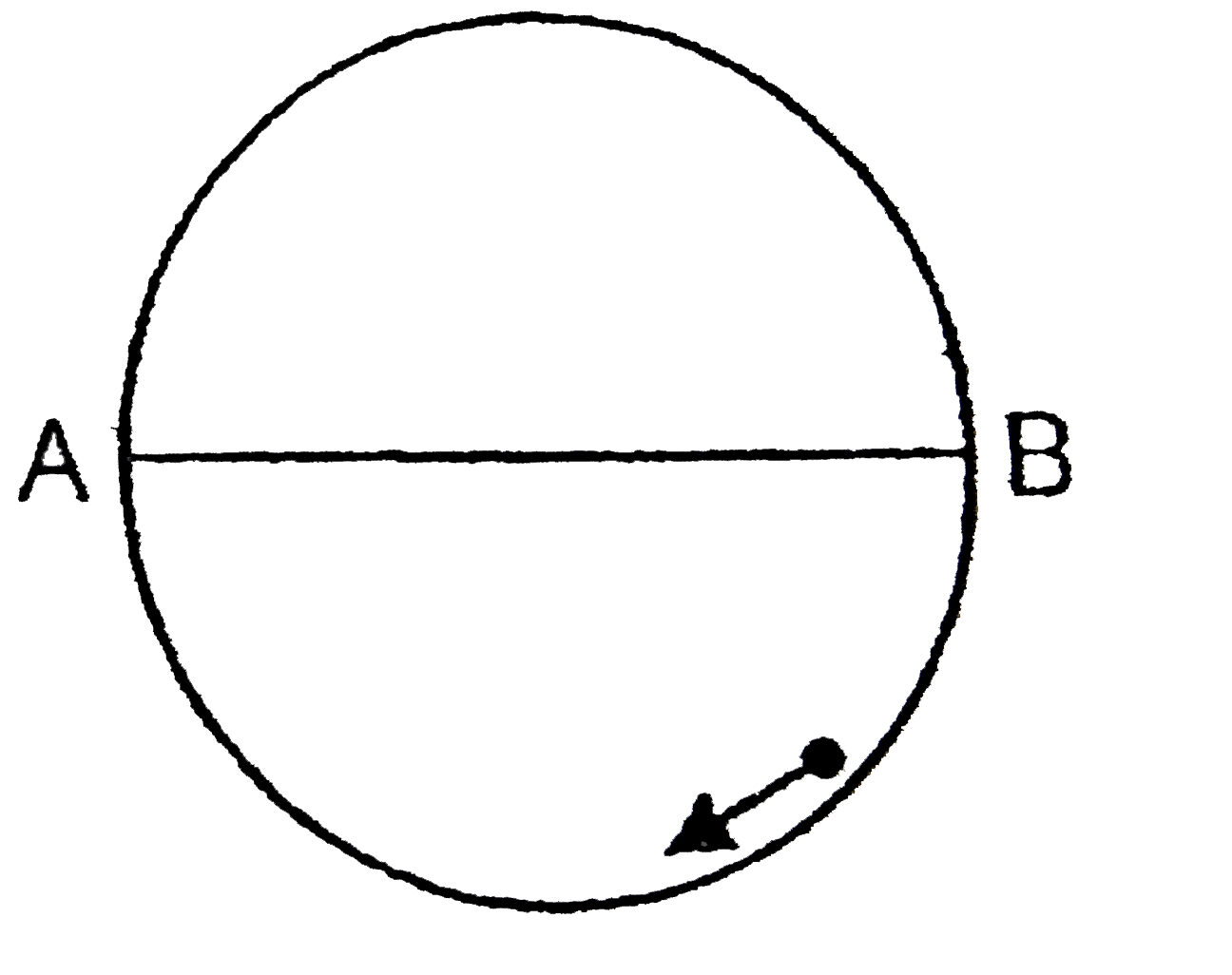 AKRB5KRC3KRD2KR
AKRB5KRC3KRD2KR
A particle of mass m=0.1kg is released from.rest from a point A of a wedge of mass M=2.4kg. The wedge is free to slide on a frictionless horizontal plane. The particle slides down the smooth face AB of the wedge. When the velocity of the wedge is 0.2ms, the velocity (in ms ) of the particle relative to the wedge is
'(##CEN_KSR_PHY_JEE_C08_E01_013_Q08##)'View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.
 View Solution
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
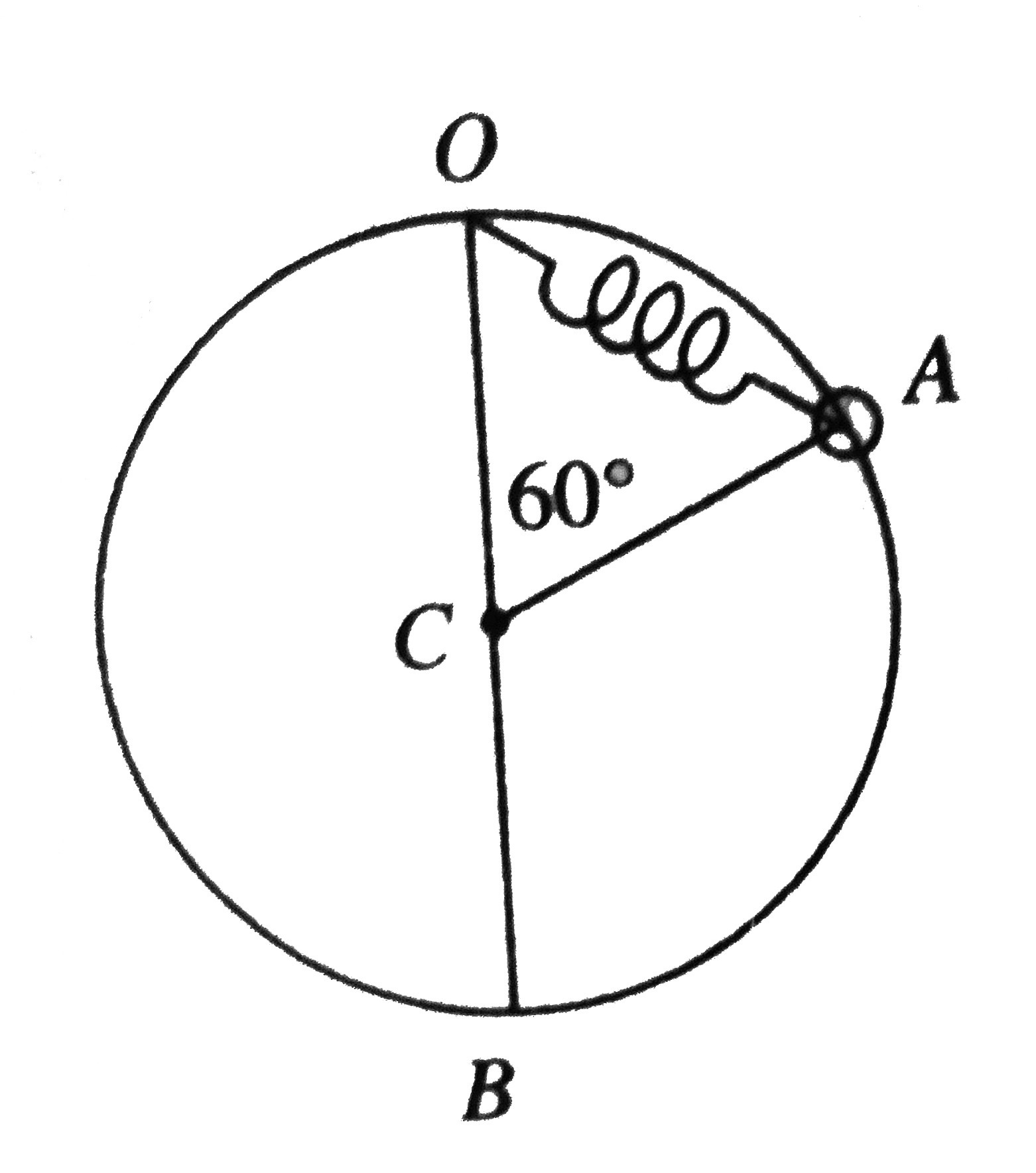 View Solution
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .
 View Solution
View Solution

