A circular loop with N turns has radius r . It lies in the x-y plane carrying current I in the anti-clockwise direction . If the magnetic field in the region is →B=B0ˆi , then find the torque (→r) acting on the loop .
B0NIπr2ˆj
B0Iπr2ˆj
B0NIπr2ˆk
B0πr2atk
The correct Answer is:A
To find the torque acting on a circular loop carrying current in a magnetic field, we can follow these steps:
Step 1: Identify the Area Vector
The area vector →A for a circular loop lies perpendicular to the plane of the loop. Since the loop is in the x-y plane, the area vector points in the positive z-direction. The magnitude of the area A of the loop is given by:
A=πr2
Thus, the area vector can be expressed as:
→A=πr2^k
Step 2: Determine the Magnetic Field
The magnetic field →B in the region is given as:
→B=B0^i
This indicates that the magnetic field is directed along the x-axis.
Step 3: Calculate the Torque
The torque →τ acting on the loop can be calculated using the formula:
→τ=N→I×→A×→B
Where N is the number of turns, I is the current, and →A is the area vector.
Since the current is flowing in the anti-clockwise direction, the effective current for N turns is:
→I=NI
Now substituting the values:
→τ=NI→A×→B
Step 4: Compute the Cross Product
We need to compute the cross product →A×→B:
→A=πr2^k,→B=B0^i
Using the right-hand rule for cross products:
^k×^i=^j
Thus,
→A×→B=πr2^k×B0^i=πr2B0^j
Step 5: Final Expression for Torque
Now substituting back into the torque equation:
→τ=NI(πr2B0^j)=NIπr2B0^j
Final Answer
The torque acting on the loop is:
→τ=NIπr2B0^j
---
The area vector →A for a circular loop lies perpendicular to the plane of the loop. Since the loop is in the x-y plane, the area vector points in the positive z-direction. The magnitude of the area A of the loop is given by:
A=πr2
Thus, the area vector can be expressed as:
→A=πr2^k
The magnetic field →B in the region is given as:
→B=B0^i
This indicates that the magnetic field is directed along the x-axis.
The torque →τ acting on the loop can be calculated using the formula:
→τ=N→I×→A×→B
Where N is the number of turns, I is the current, and →A is the area vector.
→I=NI
→τ=NI→A×→B
We need to compute the cross product →A×→B:
→A=πr2^k,→B=B0^i
Using the right-hand rule for cross products:
^k×^i=^j
Thus,
→A×→B=πr2^k×B0^i=πr2B0^j
Now substituting back into the torque equation:
→τ=NI(πr2B0^j)=NIπr2B0^j
The torque acting on the loop is:
→τ=NIπr2B0^j
Topper's Solved these Questions
Similar Questions
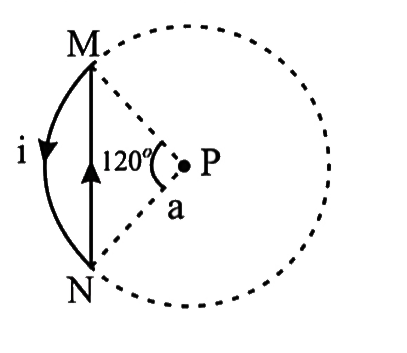
A wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View SolutionA circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
View Solution
Knowledge Check
A closed loop lying in the xy plane carries a current. If a uniformn magnetic field B is present in the region, the force acting on the loop will be zero, if B is in
Athe y-directionBthe z-directionCthe x-directionDany of the above directionsA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field→B such that vecB is perpendicular to the plane of the loop. What is the torque acting on the loop?
AzeroBir→BC3πri→BDnone of theseA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.
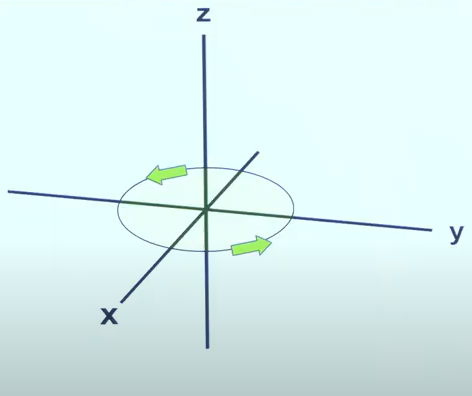
A loop when viewed from top carries on anti-clockwise current as shown. The direction of magnetic field is
View SolutionA rectangular loop carrying a current i is placed in a uniform magnetic field B. The area enclosed by the loop is A. If there are n turns in the loop, the torque acting on the loop is given by
View SolutionA circular loop of 2 turns carries a current of 5⋅0A. If the magnetic field at the centre of loop is 0⋅40mT, find the radius of the loop.
View SolutionA circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
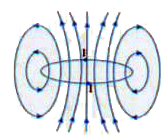
View SolutionDepict the direction of the magnetic field lines due to a circular current carrying loop.
View Solution
