What is the required condition, if the light incident on one face of a prism, does not emerge from the other face?
n<cosec (A2)
n<sec(A2)
n>secA
n>cosec (A2)
The correct Answer is:D
To solve the problem of determining the required condition for light incident on one face of a prism not to emerge from the other face, we can follow these steps:
1. Understanding the Prism Setup:
- Consider a prism with two faces: AB and AC.
- A light ray PQ is incident on face AB at an angle of incidence I.
2. Refraction at Face AB:
- When the light ray hits face AB, it refracts according to Snell's Law. Let R1 be the angle of refraction at face AB.
- The relationship can be expressed as:
n1sinI=n2sinR1
- Assuming the light is coming from air, n1=1 and n2=n (the refractive index of the prism).
3. Angle of Prism:
- The angle of the prism is denoted as A.
- According to the geometry of the prism, we have:
A=R1+R2
- Here, R2 is the angle of incidence at face AC.
4. Condition for Total Internal Reflection:
- For the light ray not to emerge from face AC, the angle R2 must be greater than the critical angle C.
- The critical angle C is defined as:
C=sin−1(1n)
- Therefore, we need:
R2>C
5. Combining the Conditions:
- Since A=R1+R2 and R2>C, we can express this condition as:
R1+R2>2C
- This implies:
A>2C
6. Using the Critical Angle:
- Substituting the expression for the critical angle, we have:
A>2sin−1(1n)
7. Final Condition:
- Taking the sine of both sides, we find:
sin(A2)>1n
- Rearranging gives:
n>csc(A2)
Conclusion:
The required condition for the light incident on one face of a prism not to emerge from the other face is:
n>csc(A2)
- Consider a prism with two faces: AB and AC.
- A light ray PQ is incident on face AB at an angle of incidence I.
- When the light ray hits face AB, it refracts according to Snell's Law. Let R1 be the angle of refraction at face AB.
- The relationship can be expressed as:
n1sinI=n2sinR1
- Assuming the light is coming from air, n1=1 and n2=n (the refractive index of the prism).
- The angle of the prism is denoted as A.
- According to the geometry of the prism, we have:
A=R1+R2
- Here, R2 is the angle of incidence at face AC.
- For the light ray not to emerge from face AC, the angle R2 must be greater than the critical angle C.
- The critical angle C is defined as:
C=sin−1(1n)
- Therefore, we need:
R2>C
- Since A=R1+R2 and R2>C, we can express this condition as:
R1+R2>2C
- This implies:
A>2C
- Substituting the expression for the critical angle, we have:
A>2sin−1(1n)
- Taking the sine of both sides, we find:
sin(A2)>1n
- Rearranging gives:
n>csc(A2)
The required condition for the light incident on one face of a prism not to emerge from the other face is:
n>csc(A2)
Topper's Solved these Questions
Similar Questions
What is the required condition, if the light incident on one face, does not emerge from the other face ?
View SolutionThe angle at which a ray of light be incident on one face of an equilateral prism,so that the emergent ray may graze the second surface of the prism is πx rad.then find "x" ."(mu=2)]
View Solution
Knowledge Check
Choose the most appropriate graph of iminv/sA, for a light ray which is incident on one face of a prism and is coming out from the opposite face (without TIR). (The symbols have their standard meanings).
A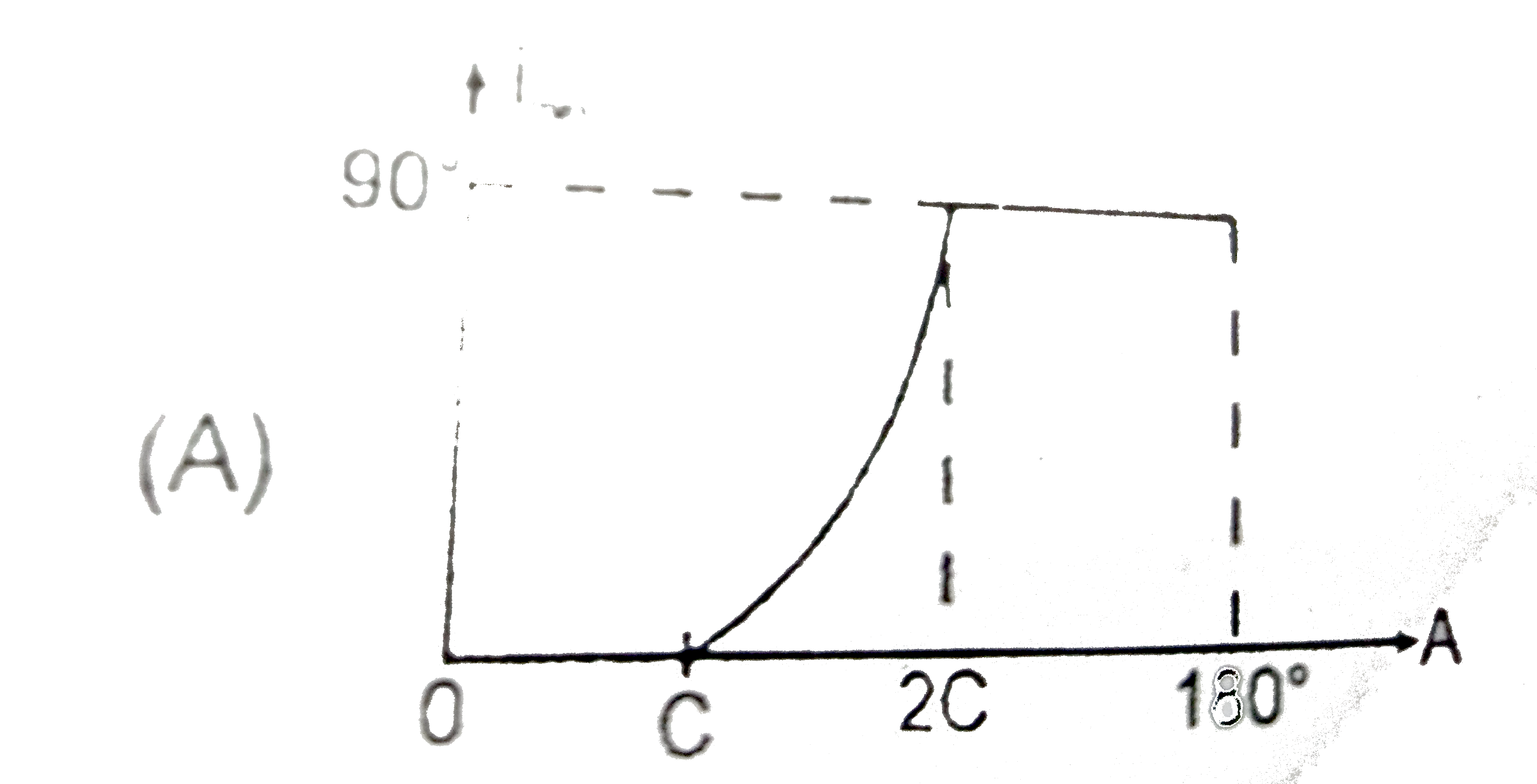 B
B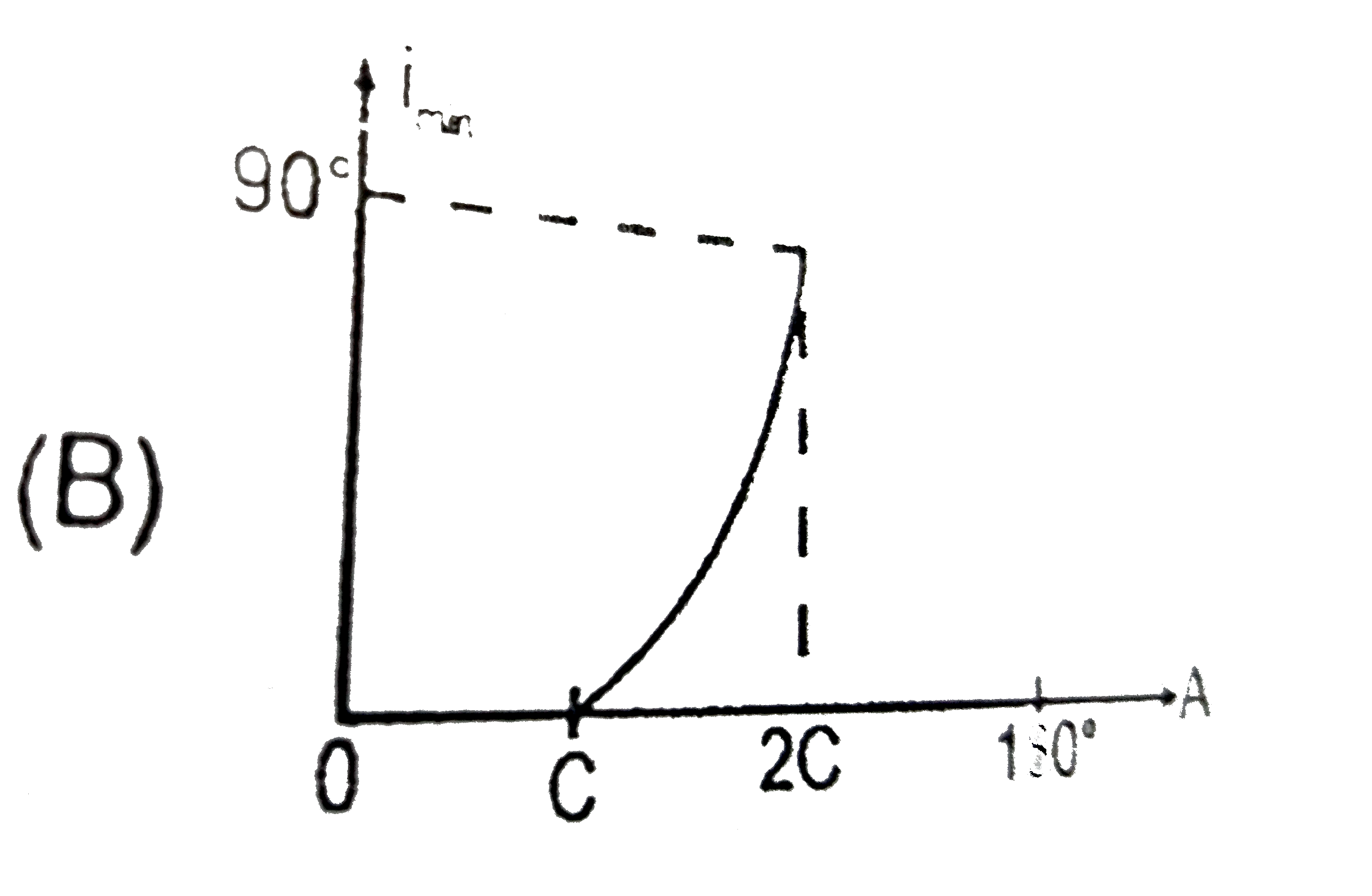 C
C D
D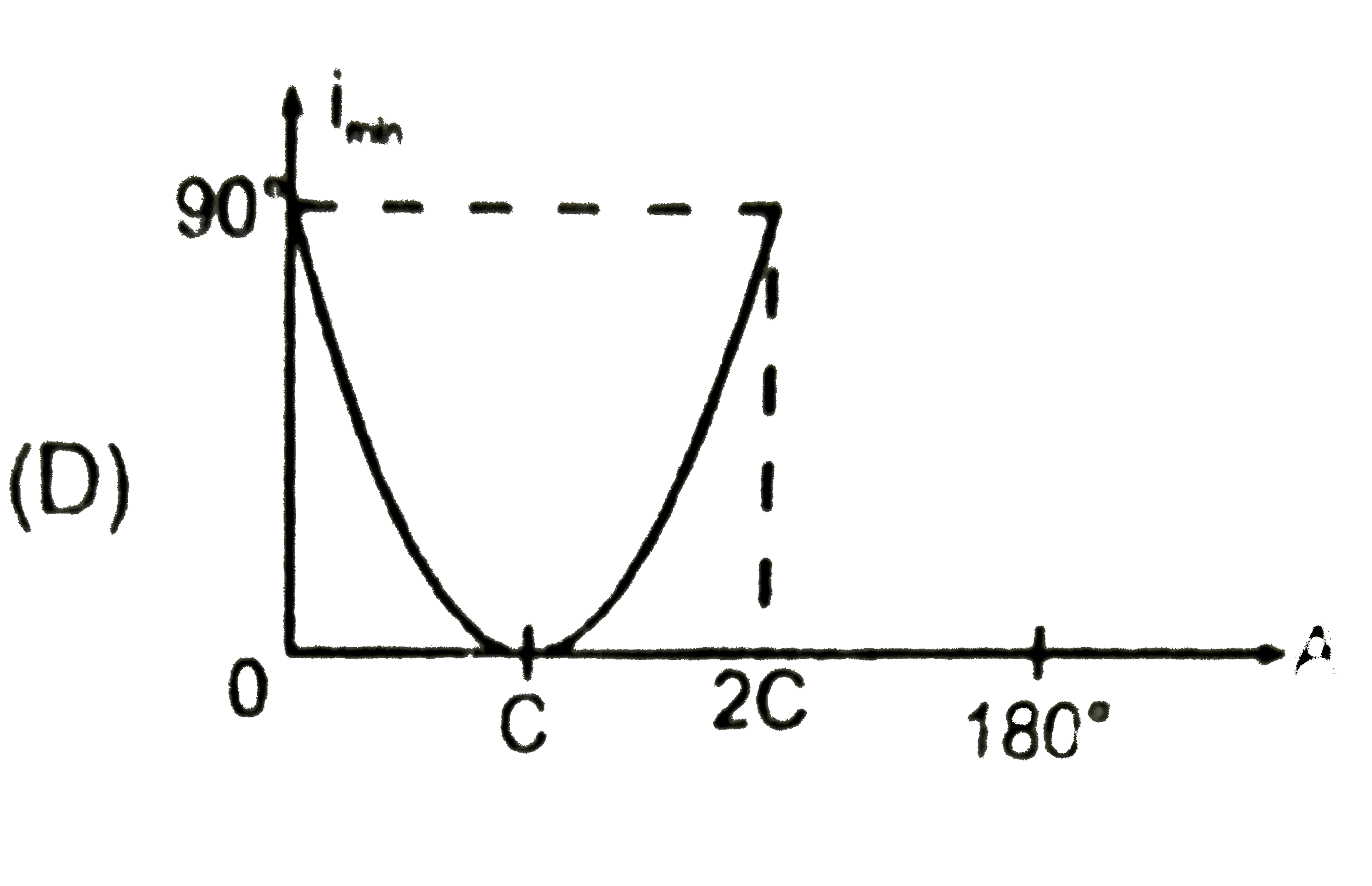
A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is
A7.5∘B5∘C15∘D2.5∘A ray of light is incident at an angle of 60∘ on one face of a 30∘ prism . The emergent ray from the prism makes an angle of 30∘ with the incident ray. The angle of emergence and refractive index of the material of the prism are-
A90∘,√3B0∘,√3C0∘,√2D90∘,√2
A ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View SolutionA ray of light is incident upon one face of a prism in a direction perpendicular to the other refracting face. The critical angle for glass – air interface is 30°. Find the angle of the prism (assuming it to be less than 90°) if the ray fails to emerge from the other face.
View SolutionA ray of light is incident at an angle of 60° on one face of a 30∘) prism. The emergent ray from the prism makes an angle of 30∘ with the incident ray. Show that the emergent ray is normal to the surface from which it emerges. Calculate the refractive index of the material of the prism.

View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle, of prism A = 60∘ and μ of material of prism is then find angle θ .

View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the meterial of prism is √2 , then the angle of deviation of the ray is
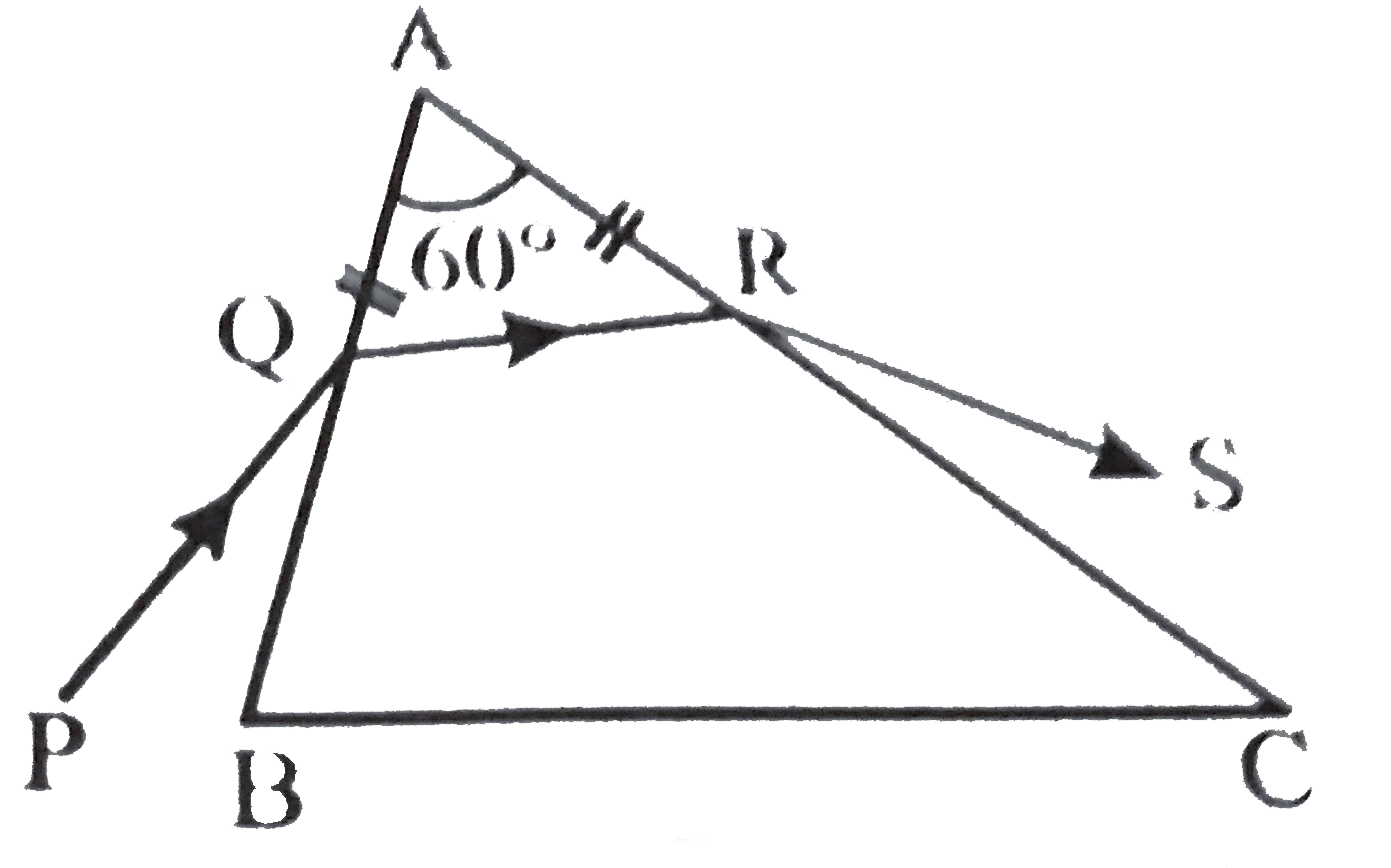
View Solution
