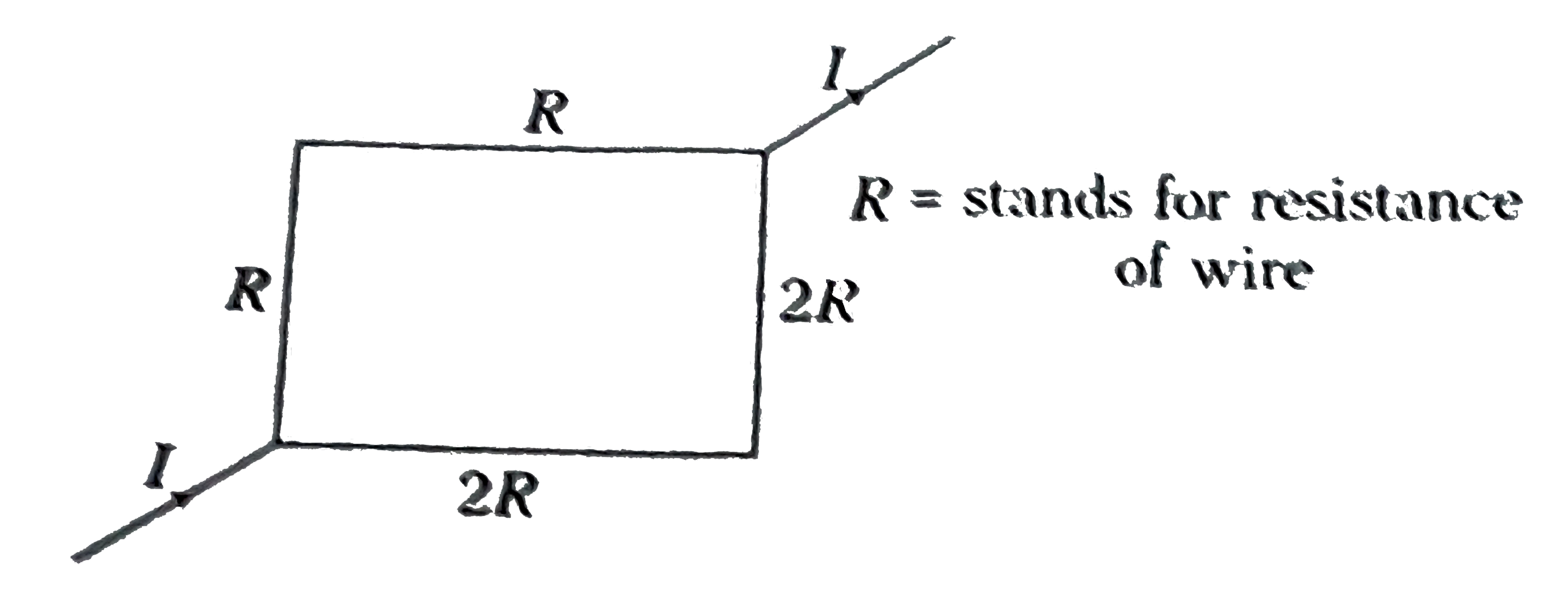
A wire in the from of a square of side 'a' carries a current i. Then the magnetic induction at the centre of the square wire is (Magnetic permeability of free space=μ0)
μ0i2πa
μ0i√2πa
2√2μ0iπa
μ0i√2πa
The correct Answer is:C
Step by step video, text & image solution for A wire in the from of a square of side 'a' carries a current i. Then the magnetic induction at the centre of the square wire is (Magnetic permeability of free space=mu_(0)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A wire in the form of a square of side '2m' carries a current 2A. Then the magentic induction at the centre of the square wire is ( magnetic permeability of free space =μ0)
Aμ02πBμ0√2πC2√2μ0πDμ0√2πA square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πa
A square wire of each side l carries a current I. What is the magnetic field at the midpoint of the square ?
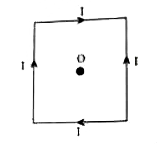
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA wire in the from of a circular loop of one turn carrying a current produces a magnetic fild B at the centre. If the same wire is looped into a coil of two turns and carreis the same current, the new value of magnetic induction at the centre is
View SolutionA wire shaped to a regular hexagon of side x carries a current I ampere. Calculate the strength of the magnetic field at the centre of the hexagon.
View SolutionTwo identical wires A and B have the same length L and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If B1andB2 are the values of magnetic induction at the centre of the square respectively, then the ratio is B1B2 is
View Solution