A rat is running on ice with speed v=πms−1. Suddenly he decides to turn by 90∘ and want of keep running with the same speed throughout. What is the least amount of time (in seocnds) he needs for such a turn? Suppose that rat's feet can move independently. Coefficieny of friction between rat's feet and ice is 0.125.
(Given : π2=g)
The correct Answer is:4
To solve the problem of the rat turning 90 degrees while maintaining a constant speed on ice, we can follow these steps:
Step 1: Understand the Forces Acting on the Rat
When the rat is turning, it experiences centripetal force that allows it to change direction. The frictional force between the rat's feet and the ice provides this centripetal force.
Step 2: Set Up the Equations
The frictional force Ff can be expressed as:
Ff=μ⋅N
where μ is the coefficient of friction (0.125) and N is the normal force, which equals the weight of the rat mg (where g=π2). Thus:
Ff=μ⋅mg
Step 3: Relate the Centripetal Force to Friction
For circular motion, the centripetal force Fc required to keep the rat moving in a circle of radius r at speed v is given by:
Fc=mv2r
Setting the frictional force equal to the centripetal force gives us:
μmg=mv2r
We can cancel m from both sides:
μg=v2r
Step 4: Solve for the Radius r
Substituting g=π2 and v=π:
0.125⋅π2=π2r
Rearranging gives:
r=π20.125⋅π2=10.125=8 m
Step 5: Calculate the Distance for the Turn
The rat is making a quarter-circle turn, so the distance d traveled during the turn is:
d=14⋅2πr=14⋅2π⋅8=4π m
Step 6: Calculate the Time Taken for the Turn
Using the formula for time t:
t=dv
Substituting the values:
t=4ππ=4 seconds
Final Answer
The least amount of time the rat needs to turn 90 degrees while maintaining its speed is 4 seconds.
---
When the rat is turning, it experiences centripetal force that allows it to change direction. The frictional force between the rat's feet and the ice provides this centripetal force.
The frictional force Ff can be expressed as:
Ff=μ⋅N
where μ is the coefficient of friction (0.125) and N is the normal force, which equals the weight of the rat mg (where g=π2). Thus:
Ff=μ⋅mg
For circular motion, the centripetal force Fc required to keep the rat moving in a circle of radius r at speed v is given by:
Fc=mv2r
Setting the frictional force equal to the centripetal force gives us:
μmg=mv2r
We can cancel m from both sides:
μg=v2r
Substituting g=π2 and v=π:
0.125⋅π2=π2r
Rearranging gives:
r=π20.125⋅π2=10.125=8 m
The rat is making a quarter-circle turn, so the distance d traveled during the turn is:
d=14⋅2πr=14⋅2π⋅8=4π m
Using the formula for time t:
t=dv
Substituting the values:
t=4ππ=4 seconds
The least amount of time the rat needs to turn 90 degrees while maintaining its speed is 4 seconds.
Topper's Solved these Questions
Similar Questions
Even some seasoned roller coaster riders blanch at the thought of riding the Rotor, which is essentially a large, hollow cylinder that is rotated rapidly around its central axis. Before the ride begins, a rider enters the cylinder through a door on the side and stands on a floor, up against a canvas covered wall. The door is closed, and as the cylinder begins to turn, the rider, wall, and floor move in unison. When the rider's speed reaches some predetermined value, the floor abruptly and alarminglly falls away. The rider does not fal with it but instead is pinned to the wall while the cylinder rotates, as if an unseen (and somewhat unfriendly) agent is pressin the body to the wall. Later, the floor is eased back to the rider's feet, the cylinder slows. and the rider sinks a few centimeters to regain footing on the floor. (Some riders consider all this to be fun.)
Suppose that the coefficient of static friction μs between the rider's clothing and the canvas is 0.40 and that the cylinder's radius R is 2.1 m.
a. What minimum speed v must the cylinder and rider have if the rider is not to fall when the floor drops?
b. If the rider's mass is 49 kg, what is the magnitude of the centripetal force on her?
View SolutionA 90−kg man runs up an escalator while it is not in operation in 10s. What is the average power developed by the man. Suppose the escalator is running so that the escalator steps move at a speed of 0.5m−1. What is then the power developed by the man as seen by the ground reference if he moves at the same speed relative to the escalator steps as he did when the escalator is not in operation?

View Solution
Knowledge Check
A car is moving with speed v and is taking a turn on a circular road of radius 10 m. The angle of banking is 37∘. The driver wants that car does not slip on the road. The coefficient of friction is 0.4(g=10m/sec2)
If the car were moving on a flat road and distance between the front tyres is 2 m and the height of the centre of the mass of the car is 1m from the ground, then, the minimum velocity for which car topples is :A5m/secB5√3m/secC3√5m/secD10m/secAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
In Q.1, what would be the approximate retardation to be given by jet pack along for safe landing?A5gms−2B2gms−2C4gms−2DCannot be determined1. Keep your watch accurate. For some people, moving up the time on their watch will help them get up earlier. For others, they will remember that the time on the watch is wrong and will disregard it altogether. It may be helpful to set your watch just two minutes ahead instead of five or ten.
2. Keep a clock, phone, computer or anything that displays time in each room of your house. One of the easiest ways to run late is simply by not realising that the time is passing as quickly as it is.
3. Set all your clocks and watches to the same time. Don't be an optimist. Things usually take longer than what you'd expect, even without major delays. If you have a dinner appointment at 7.30 p.m., don't think you can work till 7 p.m., then take a bath, dress and reach on time. Realistically, calculate the time you will take at each step and then add 10 minutes more to allow for unexpected delays, or you cannot get to your job in time.
4. Wake up when you are supposed to wake up. Don't hit the snooze button, keep on lying in bed, and watch TV at the very start of your day. May be try even setting your clock 10 minutes earlier than you need. If you have difficulty with this, move your alarm clock to somewhere away from your bed, that way, you have to get up to turn it off. Commit yourself to being 15 minutes early for everything. If you have to reach your place of work at 8.00, don't even tell yourself this. Just tell yourself (and everyone else who listens - but don't annoy them or make them think that they are late or early!) “I have to be at work at 7.45.” If you do this, you will be on time even with little unforeseen delays. You will be on time even with a traffic jam.
On the basis of your reading of the above passage answer the question:
We shall disregard the time displayed by our clock when we set it:A1-2 minutes aheadB3-4 minutes aheadC5 - 6 minutes aheadD15-20 minutes ahead
The mass of a bicycle rider along with the bicycle is 100 kg. he wants to cross over a circular turn of radius 100 m with a speed of 10ms−1. If the coefficient of friction between the tyres and the road is 0.6, will the rider be able to cross the turn? Take g=10ms−2.
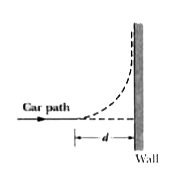
View SolutionBrake or turn? Figure depicts an overhead view of a car's path as the car travels toward a wall. Assume that the driver begins to brake the car when the distance to the wall is d=107 m, and take the car's mass a m=1400 kg, its initial speed as v0=35 m/s and the coefficient of static friction as μs=0.50. Assume that car's weight is distributed evenly on the four wheels, even during braking (a) What magnitude of static friction is needed (between tires and road) to stop the car just as it reaches the wall? (b) What is the maximum possible static friction fs,max/ (c) If the coefficient of kinetic frictic between the (sliding) tires and the road is μk=0.40, at what speed will the car hit the wall? To avoid the crash, a driver could elect to turn the car so that it just barely misses the wall, as shown in the figure. (d) What magnitude of frictional force would be required to keep the car in a circular path of radius d and at the given speed v0, so that the car moves is a quarter circle and then parallel to the wall? (e) Is the required force less than fs.max so that a circular path is possible?
View SolutionThere is a tall cylindrical building standing in a field. Radius of the cylinder is R=8m. A boy standing at A (at a distance of 10 m from the centre of the cylindrical base of the building) knows that his friend is standing at B behind the building. The line joining A and B passes through the centre of the base of the building. Distance between A and B is 50 m. A wants to throw a ball to B but he realizes that the building is too tall and he cannot throw the ball over it. He throws the ball at a speed of 20m/s such that his friend at B has to move minimum distance to catch it.

(a) What is the minimum distance that boy at B will have to move to catch the ball?
(b) At what angle to the horizontal does the boy at A throws the ball? Assume that the ball is released and caught at same height above the ground.
[Take g=10m/s2 and sin−1(0.75)≅48.6∘
View SolutionA box of mass M is at rest on a horizontal surface. A boy of mass m(<M) wants to push the box by applying a horizontal force on it. The boy knows that he will not be able to push the box as the coefficient of friction μ between his shoes and ground is almost equal to that between the box and the ground. He decides to run, acquire a speed u and then bang into the box. After hitting the box, the boy keeps pushing as hard as possible. What is the maximum distance through which the box can be displaced this way ?

View SolutionFor his 18th birthday in February Peter plants to turn a hut in the garden of his parents into a swimming pool with an artifical beach. In order to estimate the consts for heating the water and the house , peter obtains the data for the natural gas combustion and its price.
What is the total energy (in MJ) needed for Peter's "winter swimming pool" calculated in 1.3 and 1.4? How much natural gas will he need, if the gas heater has an efficiency of 90.0% ?
What are the different costs for the use of either natural gas or electricity ? Use the values given by PUC for your calculations and assume 100% efficiency for the electric heater.
Table 1: Composition of natural gas
Chemical substancemol fraction xD1H∘(KJmol−1)−1S∘(Jmol−1K−1)−1C∘p(Jmol−1K−1)−1CO2(g)0.0024−393.5213.637.1N2(g)0.01340.0191.629.1CH2(g)0.9732−74.6186.335.7C2H3(g)0.0110−84.0229.252.2H2Og−−285.870.075.3H2Og−−241.8188.833.6H2Og−0.0205.229.4
Equation
J=E(A.Δt)−1=!!λwall.ΔT.d−1, where
J= energy flow E along a temperature gradient (wall direction Z) par area A and time Δt, d-wall thickness , λwall -heat conductivity , ΔT - difference in temperature between the inside and the outside of the house.
View Solution
