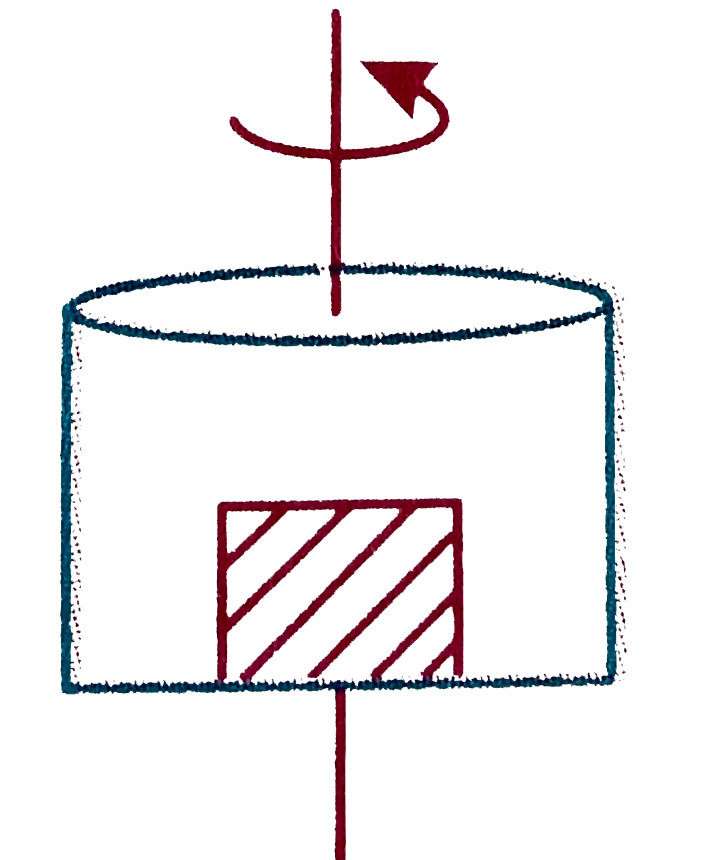
A horizontal disk is rotating with angular velocity $ω$ about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

$\frac{\sqrt{3}}{2} ω R$

$\frac{ω R}{2}$

$ω R$

$\frac{ω R}{\sqrt{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A horizontal disk is rotating with angular velocity omega about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

A $\frac{g}{2 l ω^{2}}$
B $\frac{g}{l ω^{2}}$
C $\frac{2 g}{{(l ω)}^{2}}$
D $\frac{3 g}{2 l ω^{2}}$
A horizontal disc rotates freely with angular velocity $ω$ about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
Ano friction exists between te disc and the ring
Bthe angular momentum of the system is conserved
Cthe final common angular velocity is $\frac{1}{2} ω$
Dall of the above
A disc of mass m and radius r is rotating with angular velocity, on a frictionless horizontal plane about a vertical axis passing through its centre. A ring of same mass and radius is gently placed on it in such a way that centres of both coincide. After some time it is found that both attain a common angular velocity
AIf we consider disc and ring in a single system then its angular momentum is conserved.
B $ω = \frac{ω_{0}}{3}$
CLoss in K.E. is double to that of final K.E. of the system
DLoss in K.E. is 2/3 of initial K.E. of the system.

NTA MOCK TESTS-NTA JEE MOCK TEST 84-PHYSICS

Home
Ask Doubt
Profile

A horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

A rod is rotating with angular velocity ω about axis AB. Find cosθ.

A horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.

NTA MOCK TESTS-NTA JEE MOCK TEST 84-PHYSICS

A horizontal disk is rotating with angular velocity $ω$ about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

A horizontal disc rotates freely with angular velocity $ω$ about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.