A particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
mV20Rsin2α
mV202Rcos2α
2mV20Rcos2α
mV20Rcos2α
The correct Answer is:D
To solve the problem, we need to analyze the motion of the particle moving along the internal surface of a vertical cylinder. The particle has a mass m and an initial velocity v0 forming an angle α with the horizontal.
1. Identify the Components of Velocity:
The initial velocity v0 can be broken down into two components:
- Horizontal component: v0x=v0cos(α)
- Vertical component: v0y=v0sin(α)
2. Centripetal Acceleration:
As the particle moves in a circular path along the cylinder, it experiences centripetal acceleration. The centripetal acceleration ac is given by:
ac=v2R
where v is the tangential speed of the particle.
3. Tangential Speed:
Since the particle is moving with an initial velocity v0 at an angle α, the tangential speed v at any point can be considered as the horizontal component of the velocity:
v=v0cos(α)
4. Calculate Centripetal Force:
The centripetal force Fc required to keep the particle moving in a circular path is given by:
Fc=mac=mv2R=m(v0cos(α))2R
Simplifying this, we get:
Fc=mv20cos2(α)R
5. Normal Force:
The force with which the particle acts on the cylinder wall is equal to the normal force N exerted by the wall on the particle. In this case, the normal force is equal to the centripetal force required to keep the particle in circular motion:
N=Fc=mv20cos2(α)R
Final Result:
Thus, the force with which the particle acts on the cylinder wall is:
N=mv20cos2(α)R
The initial velocity v0 can be broken down into two components:
- Horizontal component: v0x=v0cos(α)
- Vertical component: v0y=v0sin(α)
As the particle moves in a circular path along the cylinder, it experiences centripetal acceleration. The centripetal acceleration ac is given by:
ac=v2R
where v is the tangential speed of the particle.
Since the particle is moving with an initial velocity v0 at an angle α, the tangential speed v at any point can be considered as the horizontal component of the velocity:
v=v0cos(α)
The centripetal force Fc required to keep the particle moving in a circular path is given by:
Fc=mac=mv2R=m(v0cos(α))2R
Simplifying this, we get:
Fc=mv20cos2(α)R
The force with which the particle acts on the cylinder wall is equal to the normal force N exerted by the wall on the particle. In this case, the normal force is equal to the centripetal force required to keep the particle in circular motion:
N=Fc=mv20cos2(α)R
Thus, the force with which the particle acts on the cylinder wall is:
N=mv20cos2(α)R
Topper's Solved these Questions
Similar Questions
A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
View SolutionA particle moves from rest at A on the surface of a smooth circular cylinder of radius r as shown. At B it leaves the cylinder. Find the value of 4cosα3sinβ
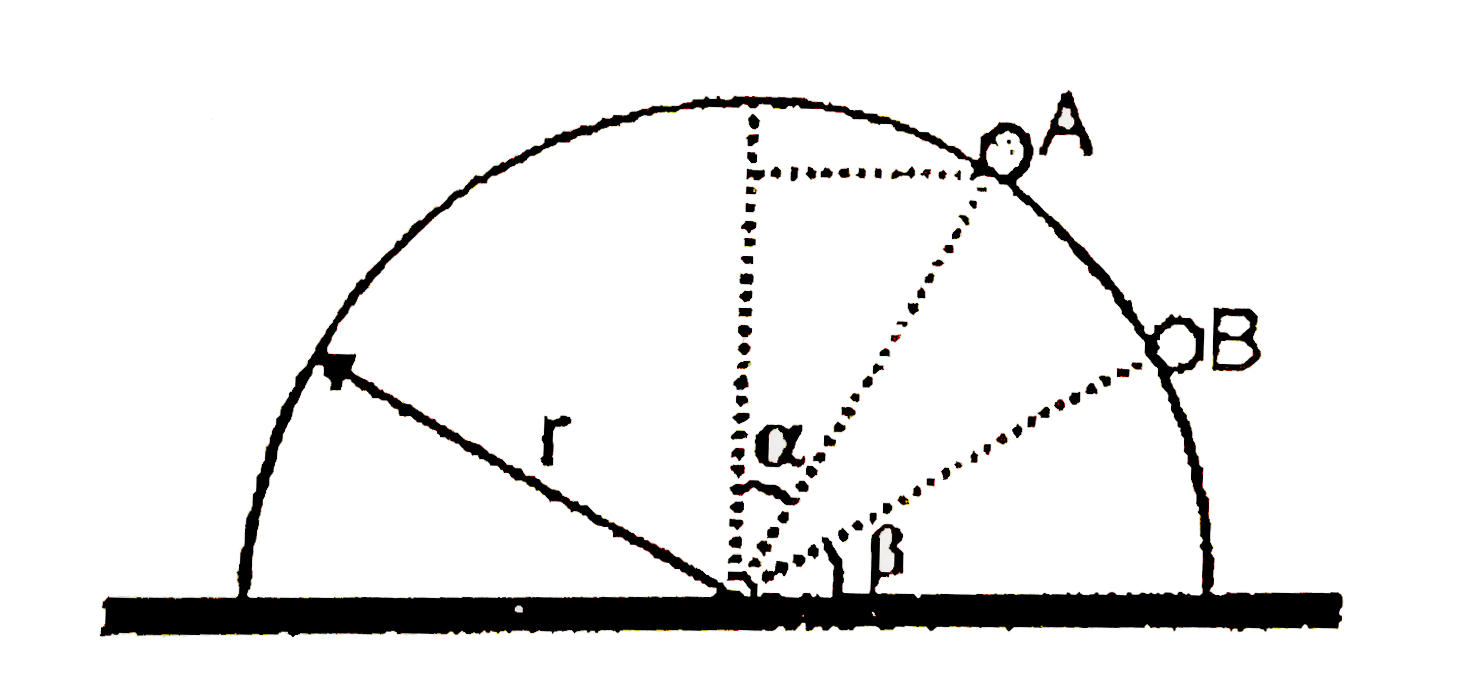
View Solution
Knowledge Check
A particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
Azero if the particle moves with uniform speed vB√2mv2πR if the particle moves with uniform speed vC√2mv2πR if the particle moves with uniform speed vDma if particle moves with constant tangential acceleration 'a', the initial velocity being equal to zeroA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronlyA particle of mass m is going along surface of smooth hemisphere of radius R in verticle plane. At the moment shown its speed is v. Choose correct option(s).
 Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
A particle of mass m moves along a circle of radius R. Find the modulus of the average vector of the force acting on the particle over the distance equal to a quarter of the circle, if the particle moves
(a) uniformly with velocity v,
(b) with constant tangential acceleration wτ, the initial velocity being equal to zero.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA heavy particle of mass m is in motion on a smooth surface of hemisphere of radius R and there is no friction. At the initial instant the particle is at the topmost point A and has an initial velocity v0 At what point will the particle leave the surface of the hemisphere ? Also determine the value of v0 for which the particle will leave the sphere at the initial instant.
View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v.
View Solution
