An open pipe of sufficient length is dipping in water with a speed $v$ vertically. If at any instant $l$ is lengths of tube avoca water. Then the rate at which fundamental frequency of pipe changes , is ( speed of sound = $c$ )

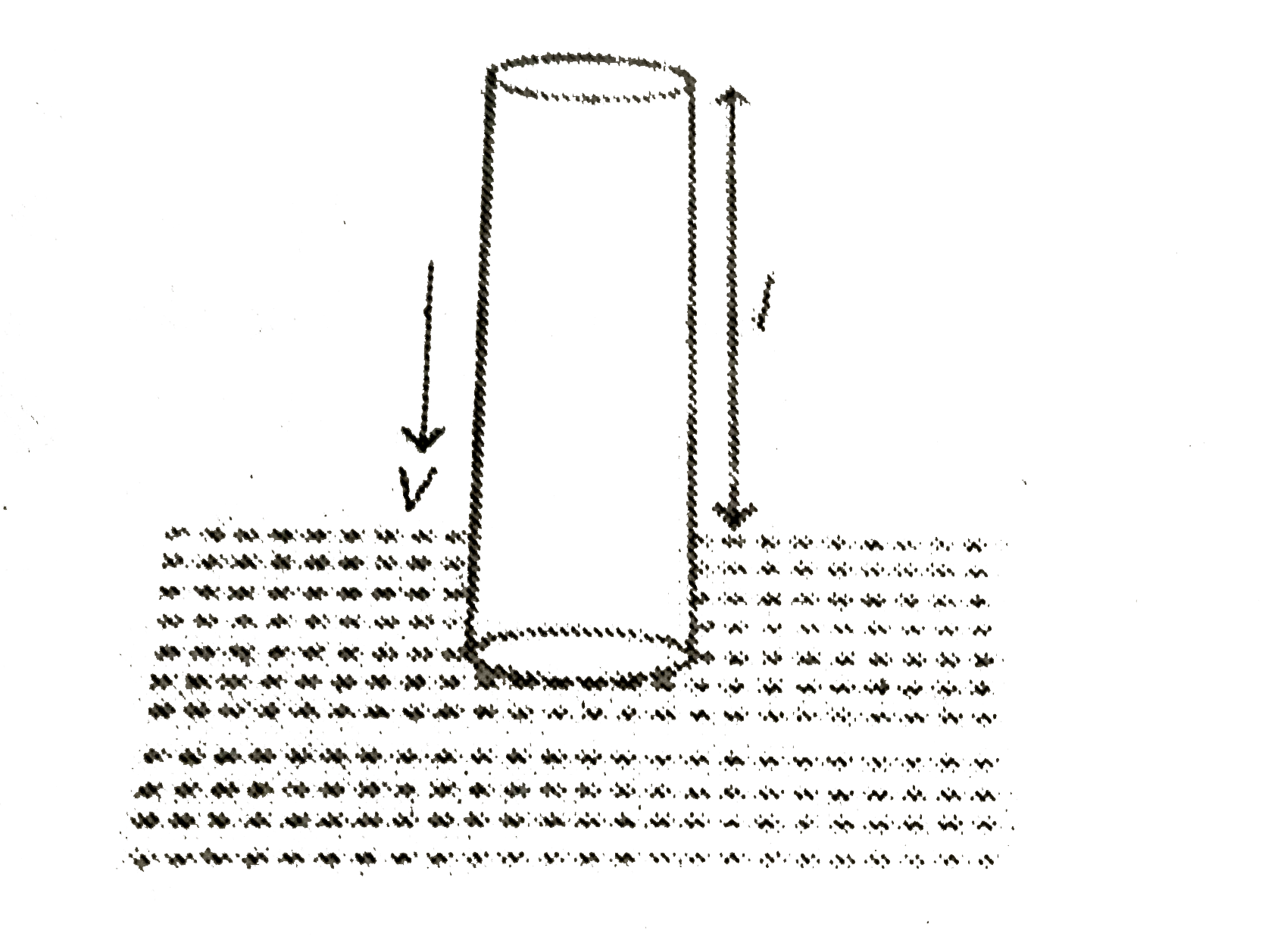
$\frac{c v}{2 l^{2}}$

$\frac{c v}{4 l^{2}}$

$\frac{c}{2 v^{2} l^{2}}$

$\frac{c}{4 v^{2} l^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for An open pipe of sufficient length is dipping in water with a speed v vertically. If at any instant l is lengths of tube avoca water. Then the rate at which fundamental frequency of pipe changes , is ( speed of sound = c) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

An open pipe of sufficient length is dipping in water with a speed V vertically if at any instant l is length of tube above water then the rate at which fundamental frequency of pipe changes is (C is the speed of sound in air )

A $\frac{C V}{2} l^{2}$
B $\frac{C V}{4} l^{2}$
C $\frac{C V}{2 v^{2} t^{2}}$
D $\frac{C V}{4 v^{2} t^{2}}$
In an organ pipe of length L open at both ends, the fundamental mode has a frequency
(where v is a speed of sound in air)
A $\frac{v}{2 L}$ and only odd harmonies are present.
B $\frac{v}{2 L}$ and only even harmonies are present.
C $\frac{v}{2 L}$ and all harmonies are present.
D $\frac{v}{4 L}$ and only odd harmonies are present.
When a closed organ pipe of length $l$ if the velocity of sound is $v$ then the fundamental frequency will be
A $\frac{V}{4 l}$ and only even harmonics are present
B $\frac{V}{2 l}$ and only odd harmonics are present
C $\frac{V}{2 l}$ and even as well as odd harmonics are present
D $\frac{V}{4 l}$ and only odd harmonics are present

NTA MOCK TESTS-NTA JEE MOCK TEST 96-PHYSICS

Home
Ask Doubt
Profile

An open pipe of sufficient length is dipping in water with a speed v vertically. If at any instant l is lengths of tube avoca water. Then the rate at which fundamental frequency of pipe changes , is ( speed of sound = c)

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

An open pipe of sufficient length is dipping in water with a speed V vertically if at any instant l is length of tube above water then the rate at which fundamental frequency of pipe changes is (C is the speed of sound in air )

In an organ pipe of length L open at both ends, the fundamental mode has a frequency (where v is a speed of sound in air)

When a closed organ pipe of length l if the velocity of sound is v then the fundamental frequency will be

NTA MOCK TESTS-NTA JEE MOCK TEST 96-PHYSICS

An open pipe of sufficient length is dipping in water with a speed $v$ vertically. If at any instant $l$ is lengths of tube avoca water. Then the rate at which fundamental frequency of pipe changes , is ( speed of sound = $c$ )

In an organ pipe of length L open at both ends, the fundamental mode has a frequency
(where v is a speed of sound in air)

When a closed organ pipe of length $l$ if the velocity of sound is $v$ then the fundamental frequency will be