A binary solution contains x1andx2 mile fraction of two components having vapour pressure p∘1andp∘2 in this pure states. The total vapour pressure above the solution is
(p∘1−P∘2)x1+P∘2
(p∘2−P∘1)x1+P∘2
(p∘1−P∘2)x1+P∘1
(p∘2−P∘1)x1+P∘1
The correct Answer is:A
To solve the problem of finding the total vapor pressure above a binary solution with given mole fractions and vapor pressures, we can follow these steps:
1. Understand the Components: We have a binary solution consisting of two components, which we will denote as Component 1 and Component 2. The mole fractions of these components in the solution are x1 and x2, respectively.
2. Define the Relationship of Mole Fractions: Since we are dealing with a binary solution, the sum of the mole fractions must equal 1:
x1+x2=1
From this, we can express x2 in terms of x1:
x2=1−x1
3. Identify the Vapor Pressures: The vapor pressures of the pure components are given as P01 for Component 1 and P02 for Component 2.
4. Calculate Partial Pressures: The partial vapor pressure of each component in the solution can be calculated using Raoult's Law, which states that the partial pressure of each component is equal to the product of its mole fraction and its pure vapor pressure:
- For Component 1:
P1=x1⋅P01
- For Component 2:
P2=x2⋅P02=(1−x1)⋅P02
5. Calculate Total Vapor Pressure: The total vapor pressure Ptotal above the solution is the sum of the partial pressures of both components:
Ptotal=P1+P2
Substituting the expressions for P1 and P2:
Ptotal=x1⋅P01+(1−x1)⋅P02
6. Simplify the Expression: We can simplify the total vapor pressure expression:
Ptotal=x1⋅P01+P02−x1⋅P02
Ptotal=P02+x1⋅(P01−P02)
Final Answer:
Thus, the total vapor pressure above the solution is given by:
Ptotal=P02+x1⋅(P01−P02)
x1+x2=1
From this, we can express x2 in terms of x1:
x2=1−x1
- For Component 1:
P1=x1⋅P01
- For Component 2:
P2=x2⋅P02=(1−x1)⋅P02
Ptotal=P1+P2
Substituting the expressions for P1 and P2:
Ptotal=x1⋅P01+(1−x1)⋅P02
Ptotal=x1⋅P01+P02−x1⋅P02
Ptotal=P02+x1⋅(P01−P02)
Thus, the total vapor pressure above the solution is given by:
Ptotal=P02+x1⋅(P01−P02)
Topper's Solved these Questions
Similar Questions
The vapour pressure of pure benzene is 22mm and that of pure toluene is 75mm at 20∘C. What is the composition of the solution of these two components that has a vapour pressure of 50mm at this temperature ? What is the composition of vapour in equilibrium with this solution ?
View SolutionA solution has a _____vapour pressure than the pure solution.
View Solution
Knowledge Check
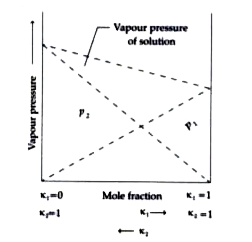
P→tal=x1p∘1+x2p∘2
=p_1^@ + (p_2^@ - p_1^@) x_2'
I. Total vapour pressure of the solution is related to the mole fraction of any one component.
II. Total vapour pressure of the solution varies exponentially with the mole fraction of component 2.
III. Depending on the vapour pressure of pure components 1 and 2, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of component 1.
select the correct staements derived from the equation.AI and IIBII and IIICIII and IDAll of the aboveIf to a solvent (vapour pressure =p∘), n moles of a non volatile solute are dissolved then the vapour pressure of the solution p is
Ap∘−p=pnBp=p∘(1−n)Cp=p∘nDNone of the aboveFor a binary ideal liquid solution, the total vapour of the solution is given as:
APtotal=P∘A+(P∘A−P∘B)XBBPtotal=P∘B+(P∘A−P∘B)XACPtotal=P∘B+(P∘B−P∘A)XADPtotal=P∘B+(P∘B−P∘A)XB
An ideal solution is prepared from A and B (both are volatile). The composition of the solution is such that the total vapour pressure is harmonic mean of vapour pressures of pure A(P∘A) and pure B(P∘B).[P∘A≠P∘B]
If xA,xB represents mole freaction of A and B in solution respectively and yA and YB represents mole fraction of A and b in vapour phase, then answer the following questions.
If the total vapour pressure is half the value mentioned in the above comprehension, then which of the following must be ture?
View SolutionThe vapour pressure of pure water at 75∘is 296torr the vapour pressure lowering due to 0.1m solute is
View SolutionWhen a liquid is completely miscible with another liquid, a homogeneous solution consisting of a single phase is formed. If such a solution is placed in a closed evacuated vessel, the total pressure exerted by the vapour, after the system attained equilibrium will be equal to the sum of partial pressures of the constituents. A solution is said to be ideal if its constituents follow Raoult's law under all conditions of concentrations, i.e., where pi is the partial pressures of the constituent i, whose mole fraction in the solution is xi and p∘i is the corresponding vapour pressure of the pure constituent. The change in the thermodynamic functions when an ideal solution is formed by mixing pure components is given by the following expression.
Δmix=G=ntotalRT∑ixiInxi ...(i)
where, ntotal is the total amount of all the constituents present in the solution.
ΔmixF=−ntotalR∑ixiInxi ......(ii)
ΔmixH=−ntotalRT∑ixiInxi−ntotalR∑ixiInxi=0 ........(iii)
ΔmixU=0 .........(iv)
Since botli the components of an ideal binary system follow Raoult's law of the entire range of the compositions, the partial pressure exerted by the vapours of these constituents over the solution will be given by
pA=xAp∘A ..........(v)
pB=xBp∘B .........(vi)
where, xA and xB are the mole fractions of the two constituents in the liquid phase and p∘A and p∘B are the respective vapour pressure of the pure constituents. The total pressure (p) over the solution will be the sum of the partial pressure. The composition of the vapour phase (yA) can be determined with the help of Dalton's law of partial pressures.
For an ideal solution in which p∘A>p∘B, the plot of total pressure (p) us the mole fraction of A at constant temperature in the vapour phase is:
View SolutionPAandPB are the vapour pressure of pure liquid components ,Aand B respectively of an ideal binary solution,If xA represents the mole fraction of component A, the total pressure of the solution will be
View SolutionRead the passage given below and answer the following questions :
Raoult's law states that for a solution of volatile liquids, the partial vapour pressure of each component of the solution is directly proportional to its mole fraction present in solution. Dalton's law of partial pressure states that the total pressure Ptotal over the solution phase in the container will be the sum of the partial pressures of the components of the solution and is given as:
Ptotal= P1+ P2
A solution of two liquids boils at a temperature more than the boiling point of either of them. What type of deviation will be shown by the solution formed in terms of Raoult' s law ?
View Solution
