Let O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is

A

3:1

B

3:2

C

2:1

D

4:3

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to find the ratio of the area of triangle ABC to the area of triangle AOC given the condition 2→OA+3→OB+4→OC=0.

Step 1: Express the position vectors
Let the position vectors of points A, B, C, and O be represented as →A, →B, →C, and →O respectively. The given equation can be rewritten as:
2→O=−3→B−4→C
From this, we can express →O in terms of →A, →B, and →C.

Step 2: Find the area of triangle AOC
The area of triangle AOC can be calculated using the formula:
AreaAOC=12|→OA×→OC|
Here, →OA=→A−→O and →OC=→C−→O.

Step 3: Find the area of triangle ABC
The area of triangle ABC can be calculated using the formula:
AreaABC=12|→AB×→AC|
Where →AB=→B−→A and →AC=→C−→A.

Step 4: Use the given condition
From the given condition 2→OA+3→OB+4→OC=0, we can find the coefficients that relate the areas of the triangles. The coefficients 2, 3, and 4 correspond to the areas of triangles AOC, BOC, and AOB respectively.

Step 5: Calculate the ratio of areas
The ratio of the area of triangle ABC to the area of triangle AOC can be derived from the coefficients:
AreaABC=AreaAOB+AreaAOC+AreaBOC
Given that the areas are proportional to the coefficients, we can express:
AreaAOB:AreaAOC:AreaBOC=2:4:3
Thus, the area of triangle AOC is 4k and the area of triangle ABC is 2k+4k+3k=9k.

Step 6: Final Ratio
The ratio of the area of triangle ABC to the area of triangle AOC is:
AreaABCAreaAOC=9k4k=94

Conclusion
Thus, the ratio of the area of triangle ABC to the area of triangle AOC is:
94

Updated on:7/8/2024
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let ABC be a triangle and P be a point inside ABC such that −−→PA+2−−→PB+3−−→PC=→0. The ratio of the area of triangle ABC to that of APC is - (A) 2 (B) 32(C) 53 (D) 3

    A2
    B32
    C53
    D3

  • Let →AD be the angle bisector of ∠A of ΔABC such that →AD=α→AB+β→AC, then

    Aα=∣∣∣−−→AB∣∣∣∣∣∣−−→AB∣∣∣+∣∣∣−−→AC∣∣∣,β=∣∣∣−−→AC∣∣∣∣∣∣−−→AB∣∣∣+∣∣∣−−→AC∣∣∣
    Bα=∣∣∣−−→AB∣∣∣+∣∣∣−−→AC∣∣∣∣∣∣−−→AB∣∣∣,β=∣∣∣−−→AB∣∣∣+∣∣∣−−→AC∣∣∣∣∣∣−−→AC∣∣∣
    Cα=∣∣∣−−→AC∣∣∣∣∣∣−−→AB∣∣∣+∣∣∣−−→AC∣∣∣,β=∣∣∣−−→AB∣∣∣∣∣∣−−→AB∣∣∣+∣∣∣−−→AC∣∣∣
    Dα=∣∣∣−−→AB∣∣∣∣∣∣−−→AC∣∣∣,β=∣∣∣−−→AC∣∣∣∣∣∣−−→AB∣∣∣

  • The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
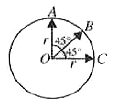    ocr_image

    Ar
    B2r
    Cr(1+√s)
    Dr(√2−1)