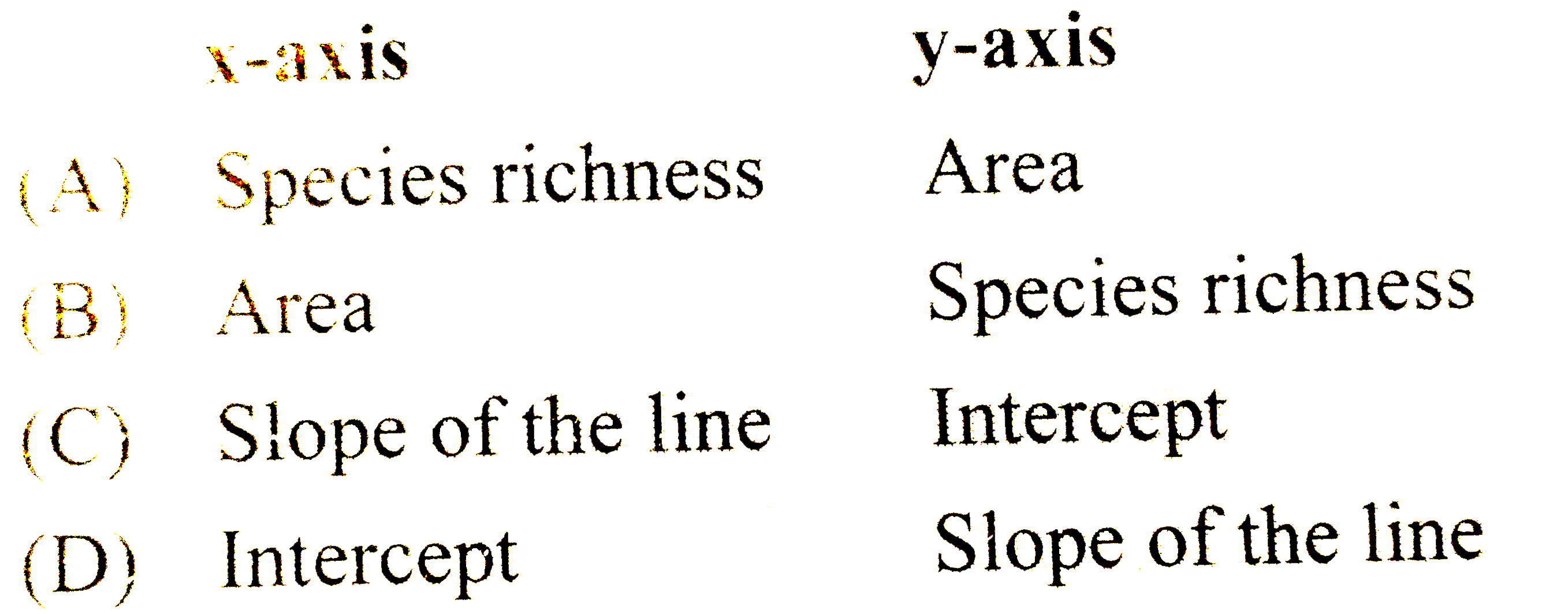In the equation of the species - area relationship , the letter 'C' and 'Z' represent:
C = Regression coefficient , Z = Y - intercept
C = Slope of the line, Z = Regression coefficient
C = Y - intercept , Z = Slope of the line (regression coefficient)
Both (B) and (C)
The correct Answer is:C
To solve the question regarding the species-area relationship and the meanings of the letters 'C' and 'Z' in the equation, we can break it down into clear steps:
1. Understanding the Species-Area Relationship:
- The species-area relationship is a concept that describes how the number of species (species richness) increases with the area being studied. This relationship was notably discussed by Alexander von Humboldt.
2. The Equation:
- The equation representing the species-area relationship is given as:
logS=logC+ZlogA
- Here, S represents species richness, A represents the area, C is a constant, and Z is a coefficient.
3. Identifying 'C':
- In the equation, C is the y-intercept when the equation is plotted on a logarithmic scale. This means that when the area A is equal to 1, the value of S (species richness) is equal to C. Thus, C represents the baseline level of species richness.
4. Identifying 'Z':
- The letter Z represents the slope of the line in the logarithmic plot. It indicates how much the species richness S increases for a unit increase in area A. A higher Z value suggests a steeper increase in species richness with increasing area.
5. Conclusion:
- Therefore, in the context of the species-area relationship:
- C is the y-intercept (constant) of the equation.
- Z is the slope of the line.
Final Answer:
- C is the y-intercept, and Z is the slope of the line in the species-area relationship equation.
- The species-area relationship is a concept that describes how the number of species (species richness) increases with the area being studied. This relationship was notably discussed by Alexander von Humboldt.
- The equation representing the species-area relationship is given as:
logS=logC+ZlogA
- Here, S represents species richness, A represents the area, C is a constant, and Z is a coefficient.
- In the equation, C is the y-intercept when the equation is plotted on a logarithmic scale. This means that when the area A is equal to 1, the value of S (species richness) is equal to C. Thus, C represents the baseline level of species richness.
- The letter Z represents the slope of the line in the logarithmic plot. It indicates how much the species richness S increases for a unit increase in area A. A higher Z value suggests a steeper increase in species richness with increasing area.
- Therefore, in the context of the species-area relationship:
- C is the y-intercept (constant) of the equation.
- Z is the slope of the line.
- C is the y-intercept, and Z is the slope of the line in the species-area relationship equation.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the equation of species-area relationship, the letter 'C' and 'Z' represent
AC = Regression coefficient, Z = y-interceptBC = slope of the line, Z = regression coefficientCC = y-intercept, Z = slope of the line (regression coefficient)DBoth B and CThe hyperbolic equation for the species area relationship is
ALogC=logS+SlogABLogS=logC+ZlogACLogS=logA+ZlogCDS=CAzSpecies area relationship was given by
AAlexander von HumboldtBPaulCMayerDBoth (a) and (b)
Species-Area relationship was given by
View SolutionIn the polt of the species - area relationship for the co-efficient z, the axis X and Y, represents
View SolutionAccording to the concept of species-area relationship.
View SolutionIn the given equation relating to species Area relationship , what does 'Z' stand for ?
logS=logc+zlogA
View SolutionThe observation of the species-area relationship was given by Humboldt after his pioneering and extensive ex-plorations in the wilderness of
View Solution