In the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
To find the displacement of the particle as it moves from point P to point C, we will follow these steps:
Step 1: Determine the coordinates of point P
From the video transcript, we know that the coordinates of point P are given as the midpoint of points B (5, 4) and O (0, 0).
To find the midpoint, we use the formula:
Midpoint=(x1+x22,y1+y22)
Here, x1=5, y1=4, x2=0, and y2=0.
Calculating the midpoint:
P=(5+02,4+02)=(2.5,2)
Step 2: Write the position vector of point P
The position vector of point P with respect to the origin O (0, 0) can be expressed as:
→P=2.5^i+2^j
Step 3: Determine the coordinates of point C
According to the transcript, the coordinates of point C are given as:
C=(0,4)
Step 4: Write the position vector of point C
The position vector of point C with respect to the origin O can be expressed as:
→C=0^i+4^j=4^j
Step 5: Calculate the displacement vector
Displacement is defined as the change in position, which can be calculated using the formula:
Displacement(→D)=→C−→P
Substituting the position vectors:
→D=(0^i+4^j)−(2.5^i+2^j)
→D=(0−2.5)^i+(4−2)^j
→D=−2.5^i+2^j
Conclusion
The displacement of the particle as it moves from point P to point C is:
→D=−2.5^i+2^j meters
---
From the video transcript, we know that the coordinates of point P are given as the midpoint of points B (5, 4) and O (0, 0).
Midpoint=(x1+x22,y1+y22)
Here, x1=5, y1=4, x2=0, and y2=0.
P=(5+02,4+02)=(2.5,2)
The position vector of point P with respect to the origin O (0, 0) can be expressed as:
→P=2.5^i+2^j
According to the transcript, the coordinates of point C are given as:
C=(0,4)
The position vector of point C with respect to the origin O can be expressed as:
→C=0^i+4^j=4^j
Displacement is defined as the change in position, which can be calculated using the formula:
Displacement(→D)=→C−→P
→D=(0^i+4^j)−(2.5^i+2^j)
→D=(0−2.5)^i+(4−2)^j
→D=−2.5^i+2^j
The displacement of the particle as it moves from point P to point C is:
→D=−2.5^i+2^j meters
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)
10 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)
14 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1cm. If the particle starts from extreme position, find the displacement of the particle after π3 seconds.
View SolutionIn the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
View Solution
Knowledge Check
A particle travels from A to B path shown in figure, then the displacement of particle is :
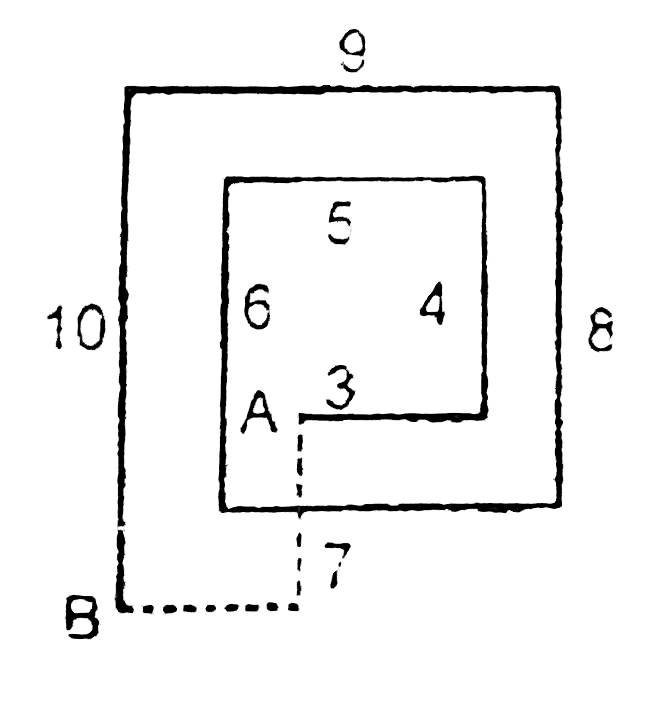 .A2√2mB4√2mC52mDnone of these
.A2√2mB4√2mC52mDnone of thesevelocity time graph of a particle is shown in figure. Find displacement of the particle.
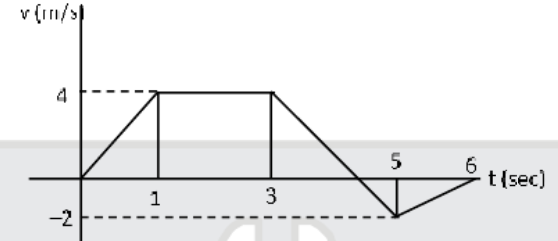 A7B11C5D15
A7B11C5D15If a particle moves from point P(2,3,5) to point Q(3,4,5). Its displacement vector be
Aˆi+ˆj+10ˆkBˆi+ˆj+5ˆkCˆi+ˆjD2ˆi+4ˆj+6ˆk
A particle starts from the origin, goes along the X-axis to the pont (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionReferring to the previous illustration, what is the
(a) acceleration of the particle?
(b) velocity of the particle at the end of 3rd second?
(c) displacement of the particio in 3 seconds?
d) displacement of the particle in 3rd second?
View SolutionIn the diagram shown, a particle is moving from the point A to the point B. Length of each arrow is 1 m and the particle is moving at a constant speed of 1ms−1 . What is the displacement of the particle?
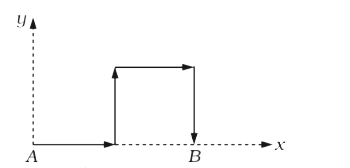
View SolutionAccleration vs time graph of a particle starting from rest is given. Find the displacement of particle in first 2 seconds.

View SolutionVelocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
View Solution
