The acceleration of a particle moving rectilinear varies with the magnitude of its velocity as a =−√v. Find its initial speed, if it stops after t0=1 sec from starting.
To solve the problem, we need to find the initial speed of a particle whose acceleration varies with velocity as a=−√v and stops after t0=1 second.
1. Understanding the relationship between acceleration and velocity:
The acceleration a can be expressed as the derivative of velocity v with respect to time t:
a=dvdt
Given that a=−√v, we can write:
dvdt=−√v
2. Rearranging the equation:
We can rearrange this equation to separate the variables v and t:
dv√v=−dt
3. Integrating both sides:
Now, we will integrate both sides. The left side will be integrated with respect to v and the right side with respect to t:
∫dv√v=∫−dt
The integral of 1√v is 2√v, and the integral of −1 with respect to t is −t. Thus, we have:
2√v=−t+C
where C is the constant of integration.
4. Finding the constant of integration:
To find C, we use the initial condition. At t=0, let the initial velocity be u:
2√u=C
Therefore, we can rewrite our equation as:
2√v=−t+2√u
5. Finding the velocity at t=1 second:
We know that the particle stops after t0=1 second, which means v=0 when t=1:
2√0=−1+2√u
This simplifies to:
0=−1+2√u
Rearranging gives:
2√u=1
6. Solving for the initial speed u:
Dividing both sides by 2:
√u=12
Squaring both sides gives:
u=(12)2=14
Final Answer:
The initial speed u of the particle is 14 m/s.
The acceleration a can be expressed as the derivative of velocity v with respect to time t:
a=dvdt
Given that a=−√v, we can write:
dvdt=−√v
We can rearrange this equation to separate the variables v and t:
dv√v=−dt
Now, we will integrate both sides. The left side will be integrated with respect to v and the right side with respect to t:
∫dv√v=∫−dt
The integral of 1√v is 2√v, and the integral of −1 with respect to t is −t. Thus, we have:
2√v=−t+C
where C is the constant of integration.
To find C, we use the initial condition. At t=0, let the initial velocity be u:
2√u=C
Therefore, we can rewrite our equation as:
2√v=−t+2√u
We know that the particle stops after t0=1 second, which means v=0 when t=1:
2√0=−1+2√u
This simplifies to:
0=−1+2√u
Rearranging gives:
2√u=1
Dividing both sides by 2:
√u=12
Squaring both sides gives:
u=(12)2=14
The initial speed u of the particle is 14 m/s.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)10videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)14videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
Tangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
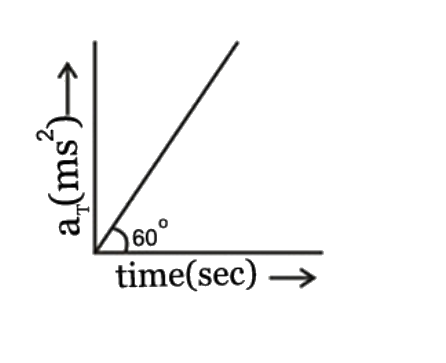 View Solution
View SolutionThe acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.View Solution
Knowledge Check
- Question 1 - Select One
The acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
Akt2+ctB1.2kt2+ctC12(kt2+ct)Dkt2+12ct - Question 2 - Select One or More
A particle is moving rectilineraly so that its acceleration is given as a=3t2+1m/s2. Its initial velocity is zero.
AThe velocity of the particle at t=1 sec will be 2m/sBThe displacement of the particle in 1 sec will be 2m.CThe particle will continoue to move in positive direction.DThe particle come back to its starting point after some time. - Question 3 - Select One
The acceleration of a particle, moving in a straight line, at time t is (2t+1)m/sec2 . If 4m/sec is the initial velocity of the particle then its velocity after 2 sec. is
A10cm/secB8cm/secC4cm/secDNone of these
The acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be
 View Solution
View SolutionThe acceleration versus time graph for a particle moving along a straight line is shown in the figure. If the particle starts from rest at t = 0, then its speed at t = 30 sec will be :
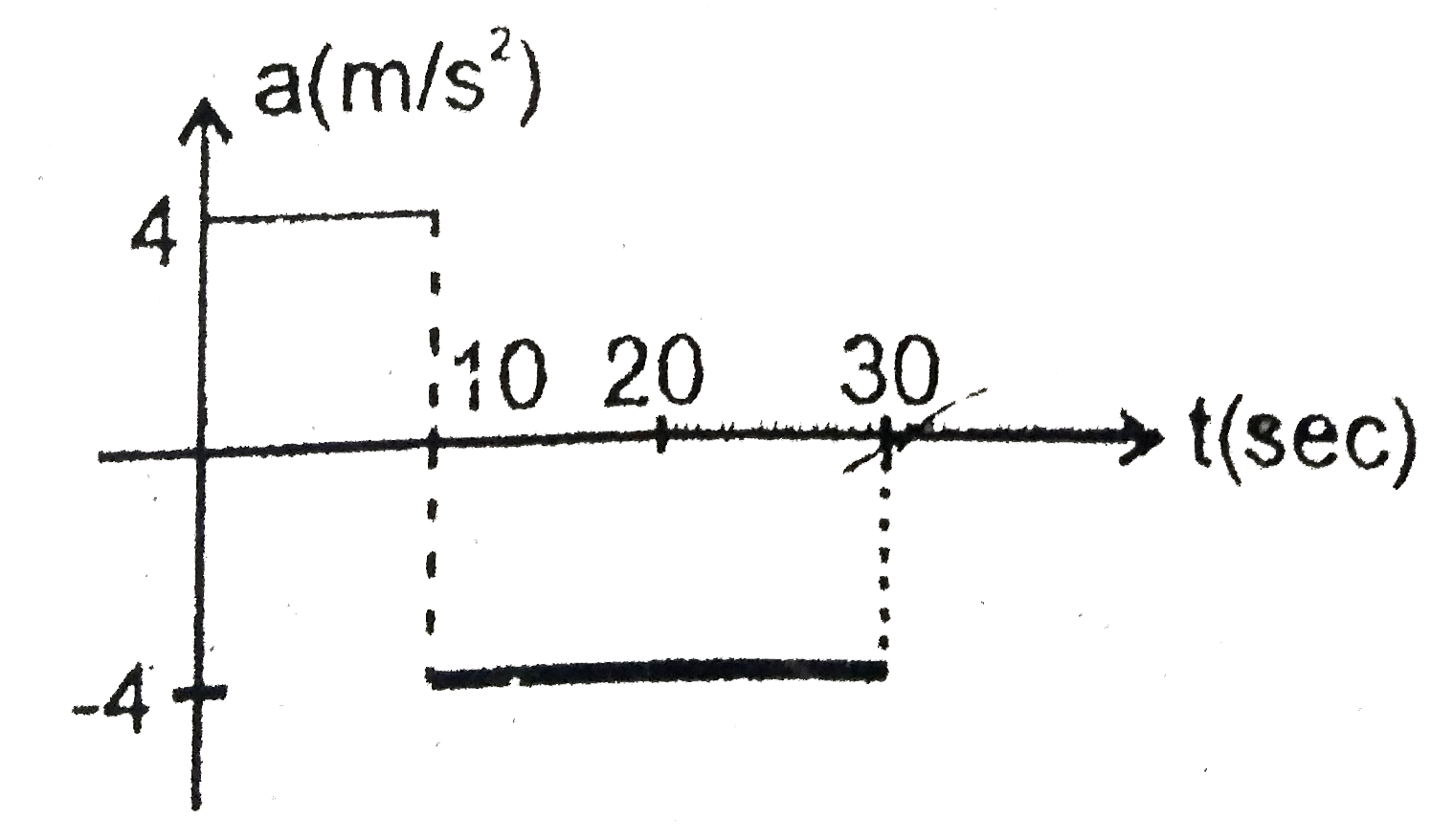 View Solution
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.View Solution

