The speed of a man in a ponds is double that of the water ina river. The man starts swimming from a polints P on the bank. What is the angle of swimming of the man so as to directly to the opposite bank?
To solve the problem, we need to determine the angle at which the man should swim in order to reach the opposite bank directly, considering the current of the river. Let's break down the solution step by step.
Step 1: Define the Variables
Let:
- Vw = speed of the water (river current)
- Vm = speed of the man in still water
- According to the problem, Vm=2Vw.
Step 2: Set Up the Diagram
Visualize the scenario:
- The river flows horizontally (let's say from left to right).
- The man starts swimming from point P on the left bank and aims to reach directly across to the opposite bank.
Step 3: Analyze the Velocities
The man swims at an angle ϕ upstream relative to the normal (perpendicular) to the bank. The velocity of the man can be broken down into two components:
- The component perpendicular to the bank: Vmcos(ϕ)
- The component parallel to the bank (against the current): Vmsin(ϕ)
Step 4: Set Up the Equation
For the man to reach the opposite bank directly, the downstream drift caused by the river must be countered by the upstream component of the man's swimming:
- The downstream drift due to the river is equal to the speed of the river Vw.
- The upstream component of the man's swimming is Vmsin(ϕ).
Thus, we can set up the equation:
Vmsin(ϕ)=Vw
Step 5: Substitute the Values
Since Vm=2Vw, substitute this into the equation:
2Vwsin(ϕ)=Vw
Step 6: Simplify the Equation
Dividing both sides by Vw (assuming Vw≠0):
2sin(ϕ)=1
Step 7: Solve for sin(ϕ)
sin(ϕ)=12
Step 8: Find the Angle ϕ
The angle whose sine is 12 is:
ϕ=30∘
Step 9: Determine the Angle from the Downstream
The angle of swimming from the downstream (which is 90∘+ϕ):
90∘+30∘=120∘
Final Answer
The angle at which the man should swim to reach the opposite bank directly is 120∘ from the downstream direction.
---
Let:
- Vw = speed of the water (river current)
- Vm = speed of the man in still water
- According to the problem, Vm=2Vw.
Visualize the scenario:
- The river flows horizontally (let's say from left to right).
- The man starts swimming from point P on the left bank and aims to reach directly across to the opposite bank.
The man swims at an angle ϕ upstream relative to the normal (perpendicular) to the bank. The velocity of the man can be broken down into two components:
- The component perpendicular to the bank: Vmcos(ϕ)
- The component parallel to the bank (against the current): Vmsin(ϕ)
For the man to reach the opposite bank directly, the downstream drift caused by the river must be countered by the upstream component of the man's swimming:
- The downstream drift due to the river is equal to the speed of the river Vw.
- The upstream component of the man's swimming is Vmsin(ϕ).
Vmsin(ϕ)=Vw
Since Vm=2Vw, substitute this into the equation:
2Vwsin(ϕ)=Vw
Dividing both sides by Vw (assuming Vw≠0):
2sin(ϕ)=1
sin(ϕ)=12
The angle whose sine is 12 is:
ϕ=30∘
The angle of swimming from the downstream (which is 90∘+ϕ):
90∘+30∘=120∘
The angle at which the man should swim to reach the opposite bank directly is 120∘ from the downstream direction.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)10videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)14videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
At what angle to the stream should a swimmer swim to reach the opposite bank as soon as possible?
View SolutionA man swims with a constant absolute velocity irrespective of the current in water. He can swim from a point P on one bank of river to a point Q just opposite the other in time t when the water is still. He takes time t1 to swim across along the same straight path PQ when the river flows down with a uniform velocity . The river velocity is btt1√(t21−t2)
where b is the breadth PQ of the river.View Solution
Knowledge Check
- Question 1 - Select One
In a lake, stream direction is as shown in the figure. A man starting from the point P on the bank wants to move to the
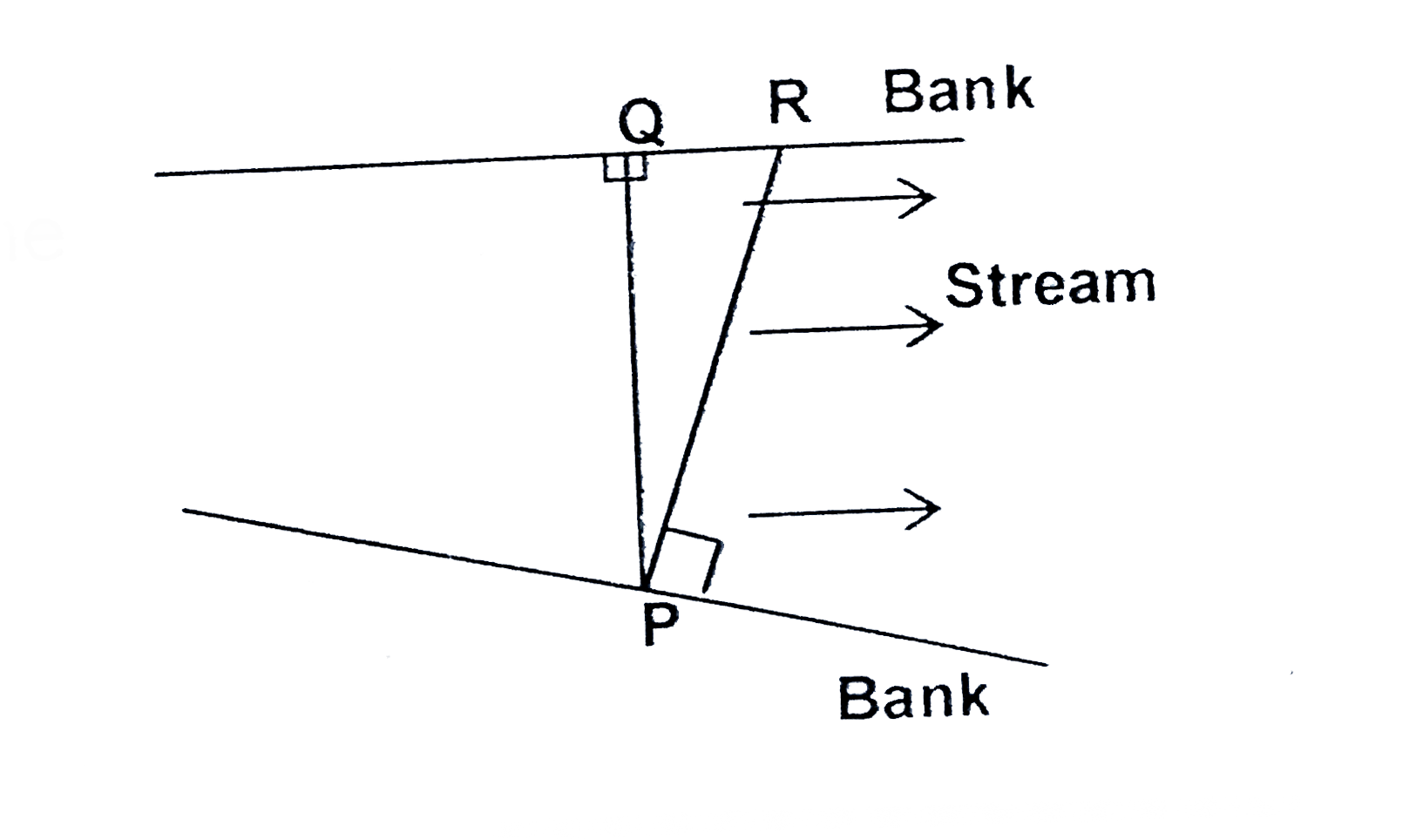 Aalong PQBalong PRCIn a direction in between PQ and PRDin all cases he would reach at the same time
Aalong PQBalong PRCIn a direction in between PQ and PRDin all cases he would reach at the same time - Question 2 - Select One
Inthe figure shown a river of width 4km is flowing with the speed of 5km/h. A swimmer whose swimming speed relative to the water is 4km/h, starts swimming from a points on a bank. On the other bank 5 is a point which is directly opposite to A. What minimum distance (in km) the swimmer will have to walk on the other bank to reach the point B.
 A2B3C4D5
A2B3C4D5 - Question 3 - Select One
In the figure shown a river of width 4km is flowing with speed of 5kim/h. A swimmer whose swimming speed relative to the wter is 4km/h, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (inkm) the swimmer will have to walk on the other bank to reach the point B.
 A2B3C4D5
A2B3C4D5
In the previous problem, How far from the point directly opposite to the starting point does the man reach the opposite bank
View SolutionIf speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
View SolutionA man can swim in still water with a speed of 3m/s x and y axis are drawn along and normal to the bank of river flowing to right with a speed of 1m/s. The man starts swimming from origin O at t = 0 second. Assume size of man to be negligible. Find the equation of locus of all the possible points where man can reach at t = 1 sec
 View Solution
View SolutionA swimmer can swim in still water with speed v and the river is flowing with speed v/2. What is the ratio of the time taken to swimming across the river in shortest time to that of swimming across the river over the shortest distance ?
View SolutionIn a river of 20 m width. Half part of river flows with speed 10m/sec and remaining half part flows with 20m/sec as shown in figure. A man starts to swim from A and reaches to point B in 10 sec. Man swims with speed Vm with respect to river at an angle θ with line AB. Then, angle θ will be : (man swims with constant speed and in same direction with respect to river throughout the motion):
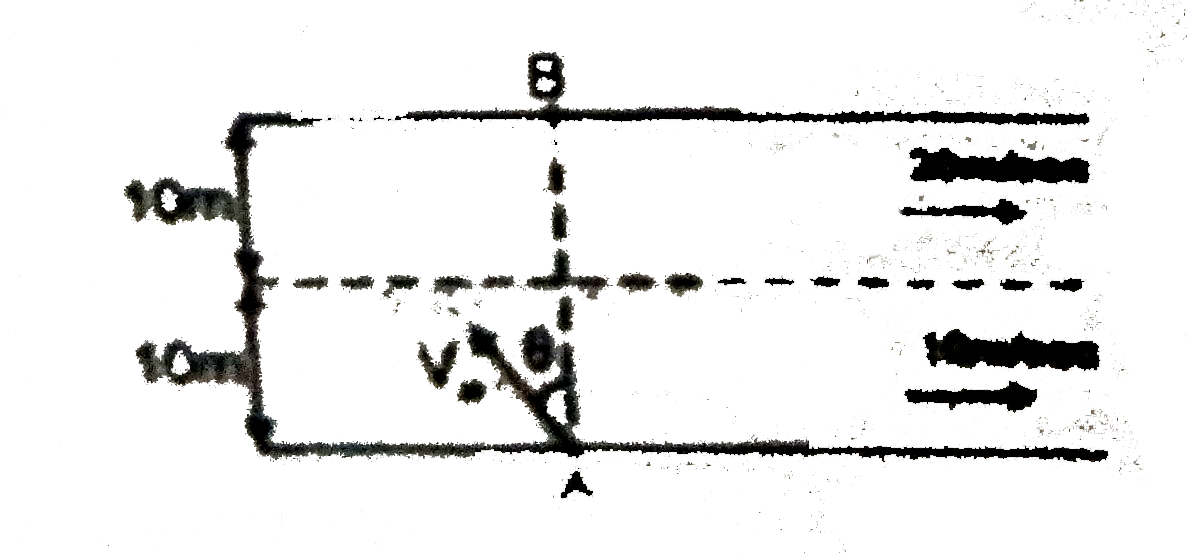 View Solution
View Solution

