At what angle to the stream should a swimmer swim to reach the opposite bank as soon as possible?
The correct Answer is:α=π/2
The speed of the swimmer in the direction of the y-axis is a maximum, if the swims perpendicularly to the stream. This obvious, if we use a feference frame fixed relative to water.
Similar Questions
A man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .
.
View SolutionThe speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View Solution
Knowledge Check
A man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .A10∘ upstreamB20∘ upstreamC30∘ upstreamD60∘ upstream
.A10∘ upstreamB20∘ upstreamC30∘ upstreamD60∘ upstreamTwo swimmers A and B start swimming from different positions on the same bank as shown in figure.The swimmer A swims at angle 90∘ with respect to the river to reach point P.He takes 120seconds to cross the river of width 10m.The swimmer B also takes the same time to reach the point P
 Avelocity of A with respect to river is 1/6m/sBriver flow velocity is 1/4m/sCVelocity of B along y-axis with respect to earth is 1/3m/s.DVelocity of B along x-axis with respect to earth is 5/24m/s.
Avelocity of A with respect to river is 1/6m/sBriver flow velocity is 1/4m/sCVelocity of B along y-axis with respect to earth is 1/3m/s.DVelocity of B along x-axis with respect to earth is 5/24m/s.
A swimmer can swim with velocity of 12 km/h in still water. Water flowing in a river has velocity 6 km/h. The direction with respect to the direction of flow of river water he should swim in order to reach the point on the other bank just opposite to his starting point is. (Round off to the Nearest Integer)
(Find the angle in degrees)
View SolutionA swimmer wishes to reach directly opposite point on the other bank of a river,flowing with velocity 4√2ms.The swimmer can swim with 8ms in still water.The angle with the flow direction he should swim to reach the directly opposite point is (A)450 (B)900 (C)1350 (D)1500
View SolutionA boat can swim in still water with speed of 20 km/h . a river of width 500 meters flows with speed of 6 km./h. In what direction . . . . should the boat be pointed , so that it reaches the opposite bank at the point directly opposite the starting point ? Also find the time . . . . . taken. Is this the least time of crossing ?
View SolutionA swimmer can swim with speed 12 m/s in still water. Speed of river is 6 m/s. Find angle at which he should swim with downstream so that he reaches directly opposite point on other side
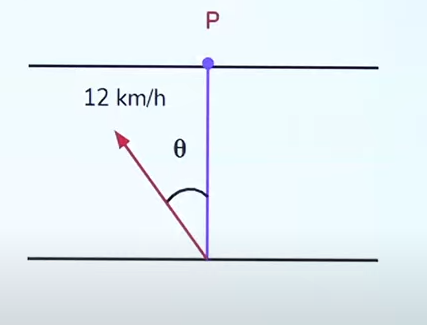
View SolutionA swimmer wants to cross a 200 m wide river which is flowing at a speed of 2 m/s. the velocity of the swimmer with respect to the river is 1 m/s. how far from the point directly opposite to the starting point does the swimmer reach the opposite bank ?
View SolutionWhat should be the angle at which a swimmer should swim to reach point C from point A (Fig.) ? The speed of the swimmer v, the speed of the stream u, and the angleβ are all known.
View Solution
