A block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0=ax. Find the kinetic energy of the block as function of x before it comes to rest.
To find the kinetic energy of a block of mass m moving with an initial velocity v0 on a rough horizontal surface where the coefficient of friction μ varies with position x as μ=μ0+αx, we can follow these steps:
1. Identify the Forces Acting on the Block:
The block experiences a frictional force due to the rough surface. The frictional force Ff can be expressed as:
Ff=μN=μ(mg)=(μ0+αx)mg
2. Determine the Work Done by Friction:
The work done by the friction force as the block moves from x=0 to x is given by:
W=−∫x0Ffdx=−∫x0(μ0+αx)mgdx
This integral can be separated:
W=−mg(∫x0μ0dx+∫x0αxdx)
3. Calculate the Integrals:
- The first integral:
∫x0μ0dx=μ0x
- The second integral:
∫x0αxdx=αx22
Thus, the work done by friction becomes:
W=−mg(μ0x+αx22)
4. Apply the Work-Energy Theorem:
According to the work-energy theorem, the work done by all forces is equal to the change in kinetic energy:
W=Kf−Ki
Where Ki=12mv20 is the initial kinetic energy and Kf is the final kinetic energy at position x. Therefore, we can write:
−mg(μ0x+αx22)=Kf−12mv20
5. Rearranging for Final Kinetic Energy:
Rearranging the equation gives us:
Kf=12mv20−mg(μ0x+αx22)
Simplifying this, we have:
Kf=12mv20−mgμ0x−mgαx22
Final Result:
The kinetic energy of the block as a function of x before it comes to rest is:
Kf(x)=12mv20−mgμ0x−mgαx22
The block experiences a frictional force due to the rough surface. The frictional force Ff can be expressed as:
Ff=μN=μ(mg)=(μ0+αx)mg
The work done by the friction force as the block moves from x=0 to x is given by:
W=−∫x0Ffdx=−∫x0(μ0+αx)mgdx
This integral can be separated:
W=−mg(∫x0μ0dx+∫x0αxdx)
- The first integral:
∫x0μ0dx=μ0x
- The second integral:
∫x0αxdx=αx22
Thus, the work done by friction becomes:
W=−mg(μ0x+αx22)
According to the work-energy theorem, the work done by all forces is equal to the change in kinetic energy:
W=Kf−Ki
Where Ki=12mv20 is the initial kinetic energy and Kf is the final kinetic energy at position x. Therefore, we can write:
−mg(μ0x+αx22)=Kf−12mv20
Rearranging the equation gives us:
Kf=12mv20−mg(μ0x+αx22)
Simplifying this, we have:
Kf=12mv20−mgμ0x−mgαx22
The kinetic energy of the block as a function of x before it comes to rest is:
Kf(x)=12mv20−mgμ0x−mgαx22
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:SOLVED PROBLEMS ( OBJECTIVE)
Explore 18 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE
Explore 1 Video
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
A small bead of mass m is given an initial velocity of magnitude v0 on a horizontal circular wire. If the coefficient of kinetic friction is μk, determine the distance travelled before the collar comes to rest.
View SolutionTime varying force horizontal F=K0t is applied on a block of mass placed at rest on a rough horizontal surface ( μ is coefficient of friction).At a time t=3μmgK0 the acceleration of the block is given by a=pμg where p=...........(K0is a positive constant)
View Solution
Knowledge Check
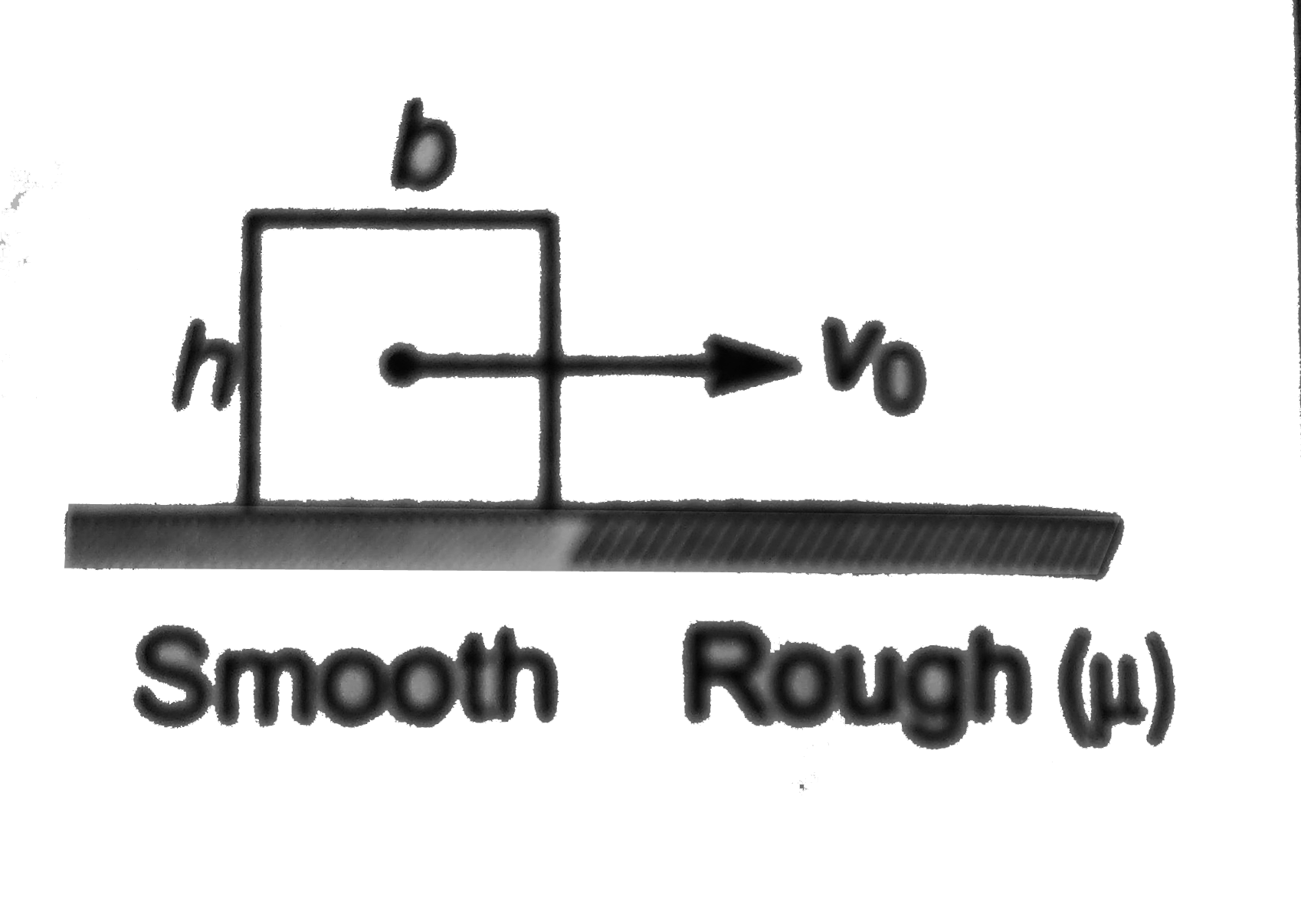
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.AThenet torque acting on the block about its COM is μmg(h)2 (clockwise)Bthe net torque acting on the block about its COM is zeroCThe net torque acting on the block about its COM is in the anticlockwise senseDNone of the above.A block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
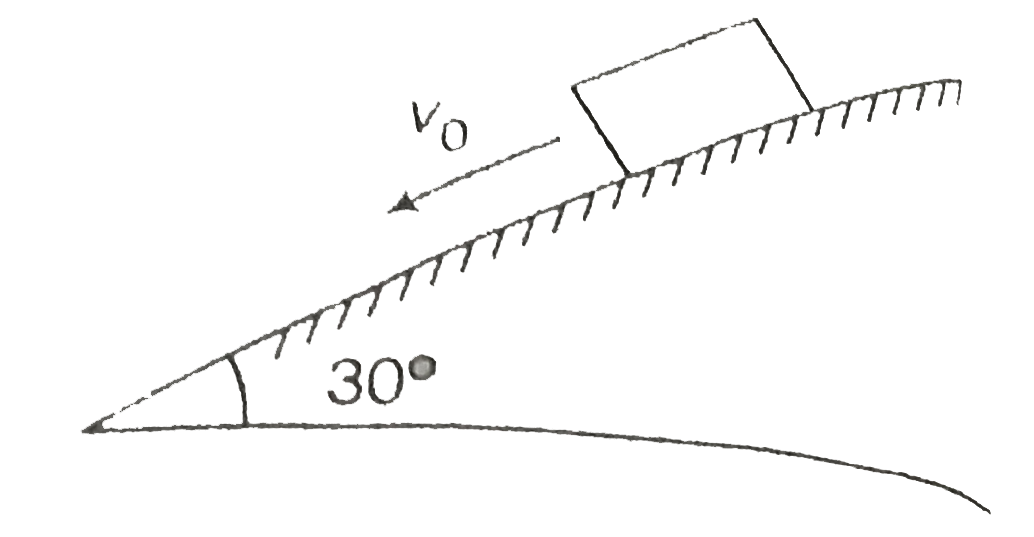 Acontinue of move down the plane with constant velocity v0Baccelerate downwardCdecelerate and come to restDfirst accelerate downward then decelerate
Acontinue of move down the plane with constant velocity v0Baccelerate downwardCdecelerate and come to restDfirst accelerate downward then decelerateA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
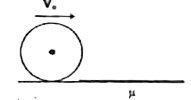 Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
A small body of mass m moving with velocity v0 on rough horizontal surface, finally stops due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient μ=0.27,m=1 kg and v0=1.5ms−1.
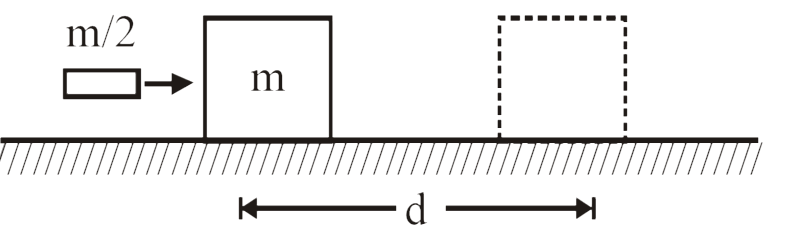
View SolutionA block of mass m rests on a rough horizontal surface (Coefficient of friction isµ). When a bullet of mass m/2 strikes horizontally, and get embedded in it, the block moves a distance d before coming to rest. The initial velocity of the bullet is k√2μgd, then the value of k is
View SolutionA small bead of mass m is given an initial velocity of magnitude v0 on a horizontal circular wire. If the coefficient of kinetic friction is μk, determine the distance travelled before the collar comes to rest.
View SolutionA block of mass m is pulled by a constant power P placed on a rough horizontal plane. The coeficient of friction between the block and surface is μ. Find the maximum velocity of the block.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View Solution
