A small block is projected with a speed v0 on a horizontal track placed on a sufficiently rough surface which turns into a semi circle ( vertical) of radius R. Find the min value of Vo so that the body will hit the point A after leaving the track at its highest point. The arrangement is shown in the figure, given that the straight part is rough & the curved path is smooth. The coefficient of friction is μ.
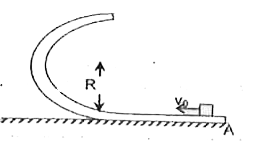
Let the block escape the point at C with a velocity V horizontally. Since it hits the initial spot A after falling through a height 2R we can write
(2R)=12gt2, whrer t= time of its fall.
⇒t=2√R/g
∴ The distance AB=2v√R/g
⇒d=2vx√R/g ...(a)
Work energy theorem is applied to the motion of the body from A to B leads ΔKE=Wf
⇒12mv2o−12mv21=μmgd
⇒vo=√v21+2μgd ...(b)
Energy conservation between B & C yields
12mv21−12mv2=mg(2R)
⇒v1=√v2+4gR ...(c)
When the block escapes C, its minimum speed v can be given as mv2R=mg
( ∴ the normal contact force =0)
⇒v=√gR ...(d)
(Note that if the particle has speed less than √gR then it will not reach to the highest point of the curvature.
By using (c) and (d) we obtain
v1=√5gR ...(e)
using (a) and (d) we obtain
d=(√gR)2(√Rg)=2R ...(f)
vo=√5gR+2μg(2R)=√(5+4μ)gR.

Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE)
18 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE
1 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
Figure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View Solution
Knowledge Check
A small block is projected into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
A B
B C
C D
D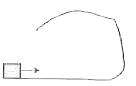
In a circus stuntman rides a motorbike in a circular track of radius R in the vertical plane. The minimum speed at highest point of track will be
A√2gRB2gRC√3gRD√gR
A small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0

View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.
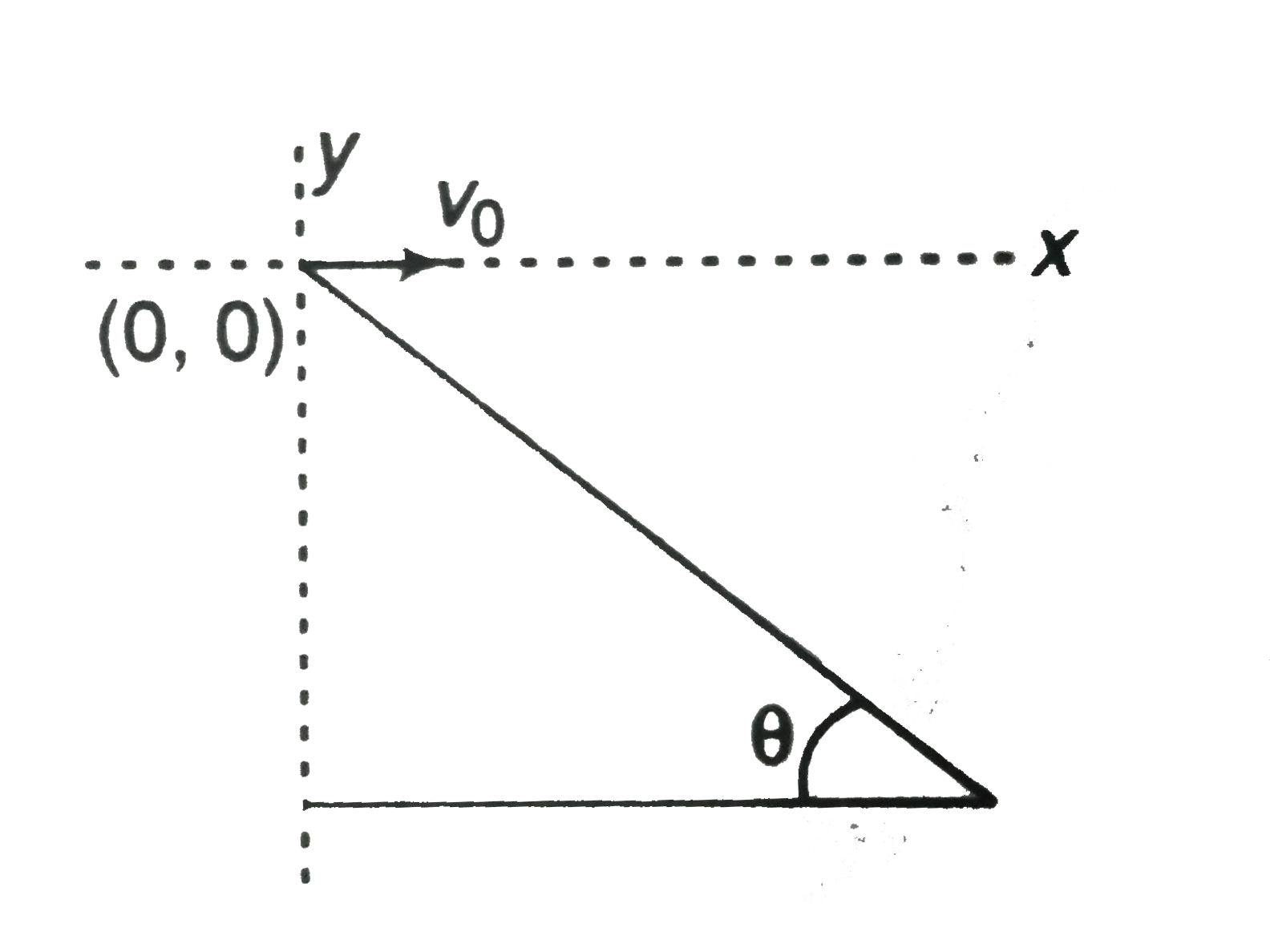
View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.

View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.

View SolutionIn a fixed quarter circular track of radius R which lies in a vertical plane, a block is released from point A and it leaves the path at point B. The radius of curvature of its trajectory when it just leaves the path will be
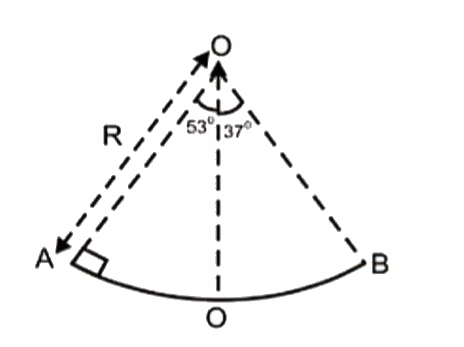
View Solution
