A stone is projected at time t=0 with a speed v0 at an angle θ with the horizontal in a uniform gravitational field. The rate of work done (P) by the gravitational force plotted against time (t) will be as.

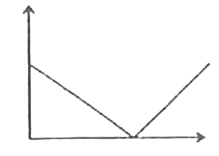
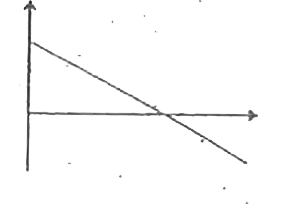
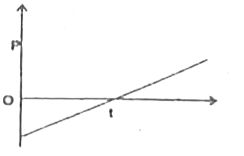
The correct Answer is:D
To solve the problem of determining the rate of work done (P) by the gravitational force plotted against time (t) for a stone projected at an angle θ with an initial speed v0, we will follow these steps:
Step 1: Understand the Motion of the Stone
The stone is projected at an angle θ with respect to the horizontal. The motion can be broken down into horizontal and vertical components. The vertical component of the initial velocity is given by:
v0y=v0sinθ
The horizontal component is:
v0x=v0cosθ
Step 2: Determine the Height (h) as a Function of Time (t)
The height h of the stone at any time t can be calculated using the kinematic equation for vertical motion:
h=v0yt−12gt2
Substituting v0y:
h=v0sinθ⋅t−12gt2
Step 3: Calculate the Work Done by Gravitational Force
The work done W by the gravitational force when the stone is at height h is given by:
W=−mgh
Substituting the expression for h:
W=−mg(v0sinθ⋅t−12gt2)
W=−mgv0sinθ⋅t+12mggt2
Step 4: Determine the Power (P)
Power P is defined as the rate of work done with respect to time:
P=dWdt
Calculating the derivative:
P=−mgv0sinθ+mggt
This simplifies to:
P=mggt−mgv0sinθ
Step 5: Analyze the Expression for Power
The expression for power P can be rewritten as:
P=mg(gt−v0sinθ)
This indicates that power is a linear function of time t with a slope of mg and a y-intercept of −mgv0sinθ.
Step 6: Graph the Power vs. Time
The graph of power P against time t will be a straight line:
- It will start below zero (negative y-intercept).
- It will have a positive slope (since mg>0).
Conclusion
The rate of work done (P) by the gravitational force plotted against time (t) will be a straight line with a negative y-intercept and a positive slope.
The stone is projected at an angle θ with respect to the horizontal. The motion can be broken down into horizontal and vertical components. The vertical component of the initial velocity is given by:
v0y=v0sinθ
The horizontal component is:
v0x=v0cosθ
The height h of the stone at any time t can be calculated using the kinematic equation for vertical motion:
h=v0yt−12gt2
Substituting v0y:
h=v0sinθ⋅t−12gt2
The work done W by the gravitational force when the stone is at height h is given by:
W=−mgh
Substituting the expression for h:
W=−mg(v0sinθ⋅t−12gt2)
W=−mgv0sinθ⋅t+12mggt2
Power P is defined as the rate of work done with respect to time:
P=dWdt
Calculating the derivative:
P=−mgv0sinθ+mggt
This simplifies to:
P=mggt−mgv0sinθ
The expression for power P can be rewritten as:
P=mg(gt−v0sinθ)
This indicates that power is a linear function of time t with a slope of mg and a y-intercept of −mgv0sinθ.
The graph of power P against time t will be a straight line:
- It will start below zero (negative y-intercept).
- It will have a positive slope (since mg>0).
The rate of work done (P) by the gravitational force plotted against time (t) will be a straight line with a negative y-intercept and a positive slope.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-I) (ASSERTION REASONING TYPE)2videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( OBJECTIVE) (LEVEL-II)19videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - ASSIGNMENT PROBLEMS ( SUBJECTIVE) (LEVEL-II & III)15videos
WORK, ENERGY AND POWER
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions
A particle is projected at time t=0 from a point O with a speed u at an angle θ to horizontal. Find the torque of a gravitational force on projectile about the origin at time t.(x,y plane is vertical plane)
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View Solution
Knowledge Check
- Question 1 - Select One
A heavy particle is projected with a velocity at an acure angle with the horizontal into a uniform gravitational field. The slope of the trajectory of the particle varies as
A B
B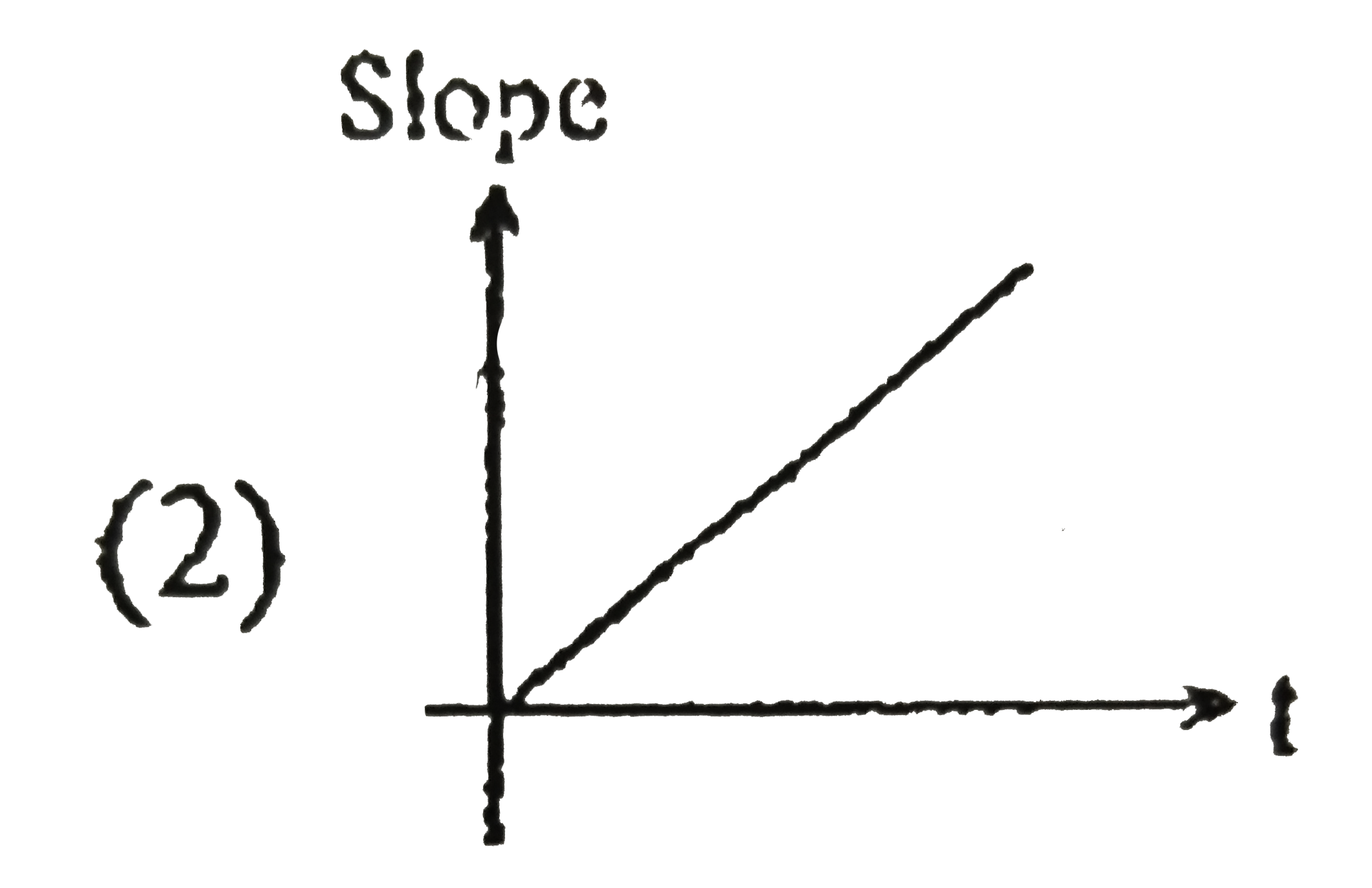 C
C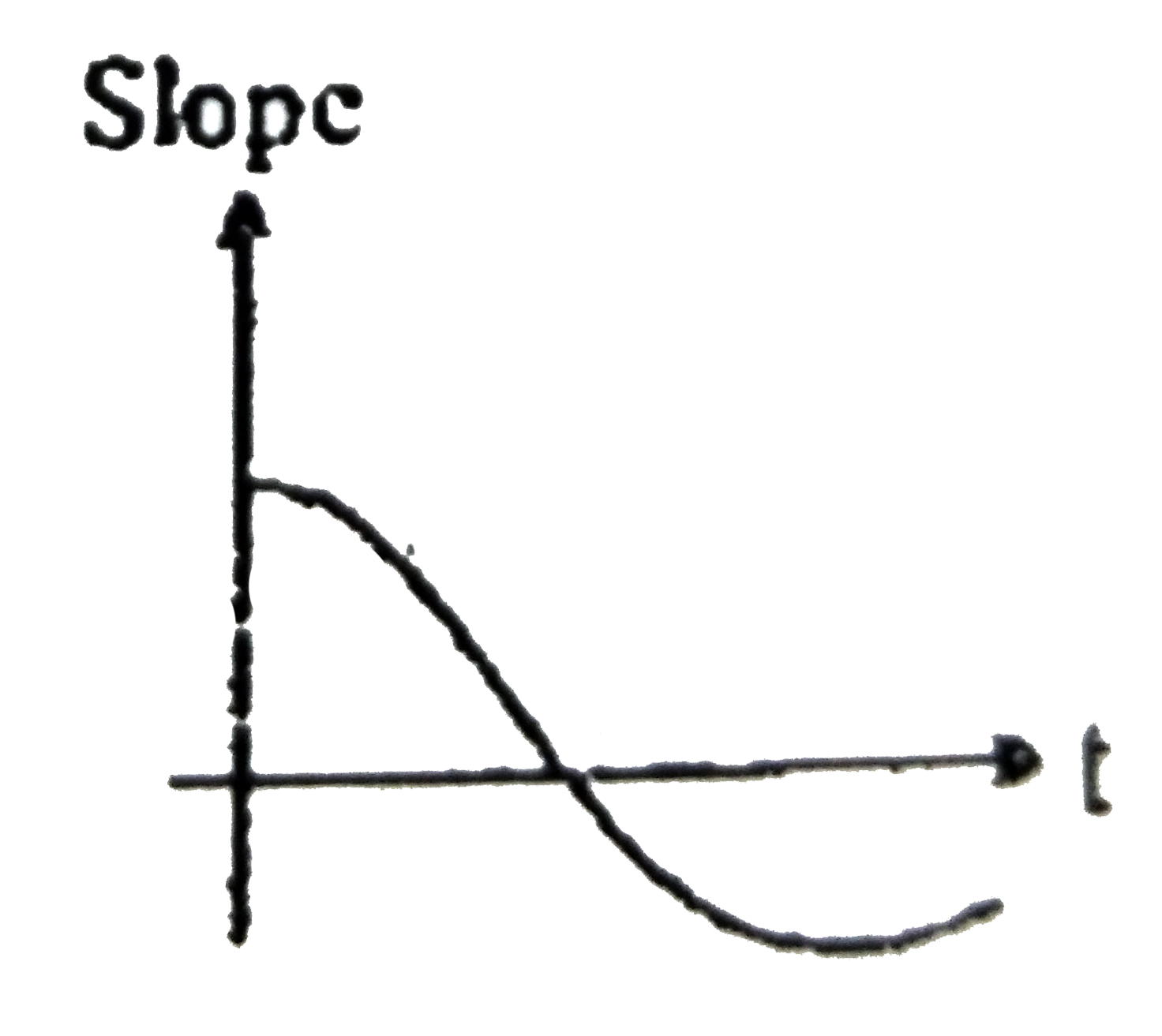 D
D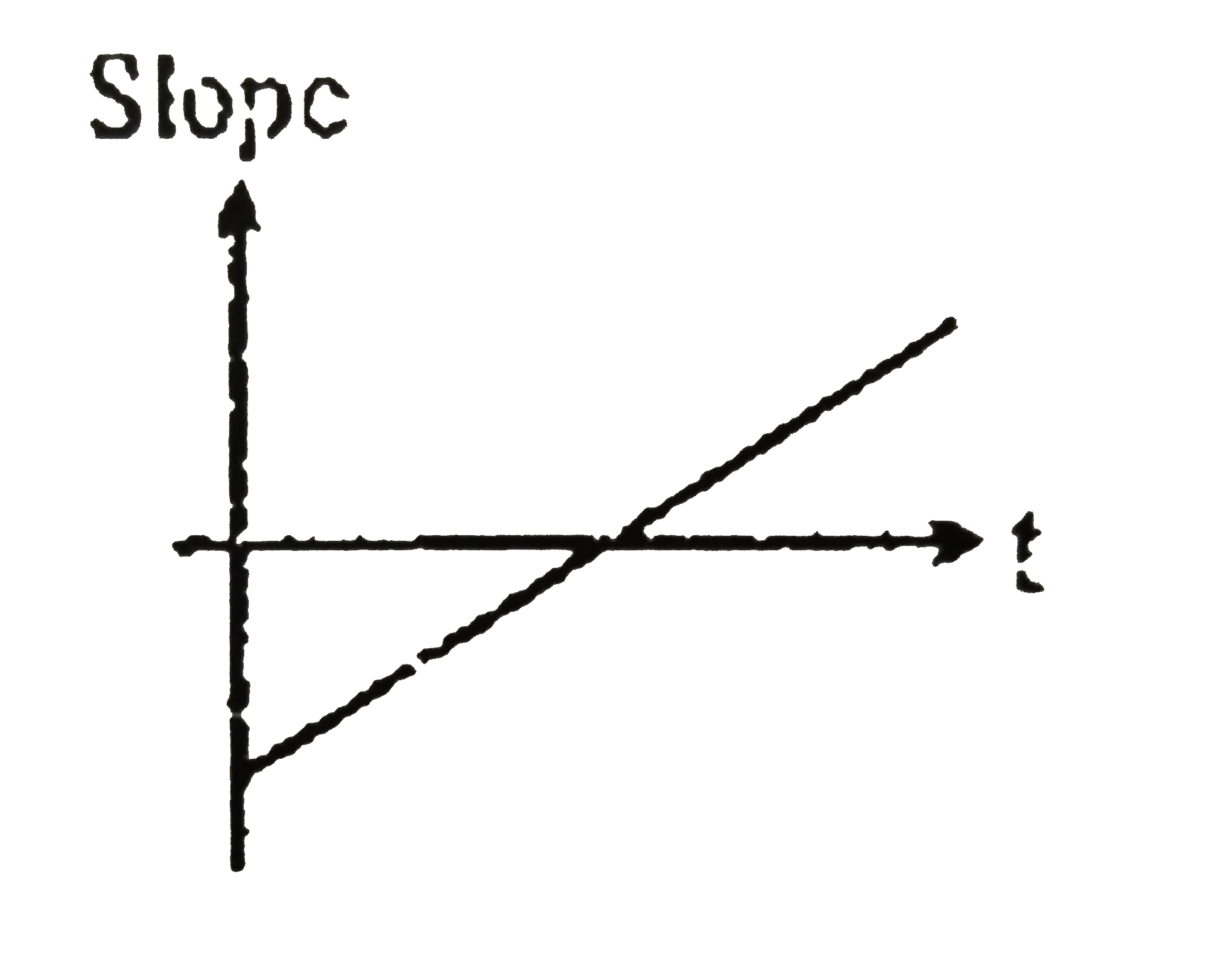
- Question 2 - Select One
A heavy particle is projected with a velocity at an angle with the horizontal into the uniform gravitational field. The slope of the trajectory of the particle varies as
A B
B C
C D
D
- Question 3 - Select One
A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
A(a) Varies linearly with timeB(b) Is constant throughoutC(c) Is negative for complete pathD(d) None of the above
A stone is projected at a speed v0 and it makes an angle θ with the horizontal. Find the angular velocity of the projectile at the time when it reaches the same level with respect to the point of projection at the time it touches the ground.
View SolutionA bode mass m is projected at an angle θ with the horizontal with an initial velocity u, the average power of gravitational force over the whole time of flight is.
View SolutionThe figure shows the velocity (v) of a particle plotted against time (t).
 View Solution
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionWhen a body is projected at an angle with the horizontal in the uniform gravitational field of the earth, the angular momentum of the body about the point of projection, as it proceeds along its path
View Solution

