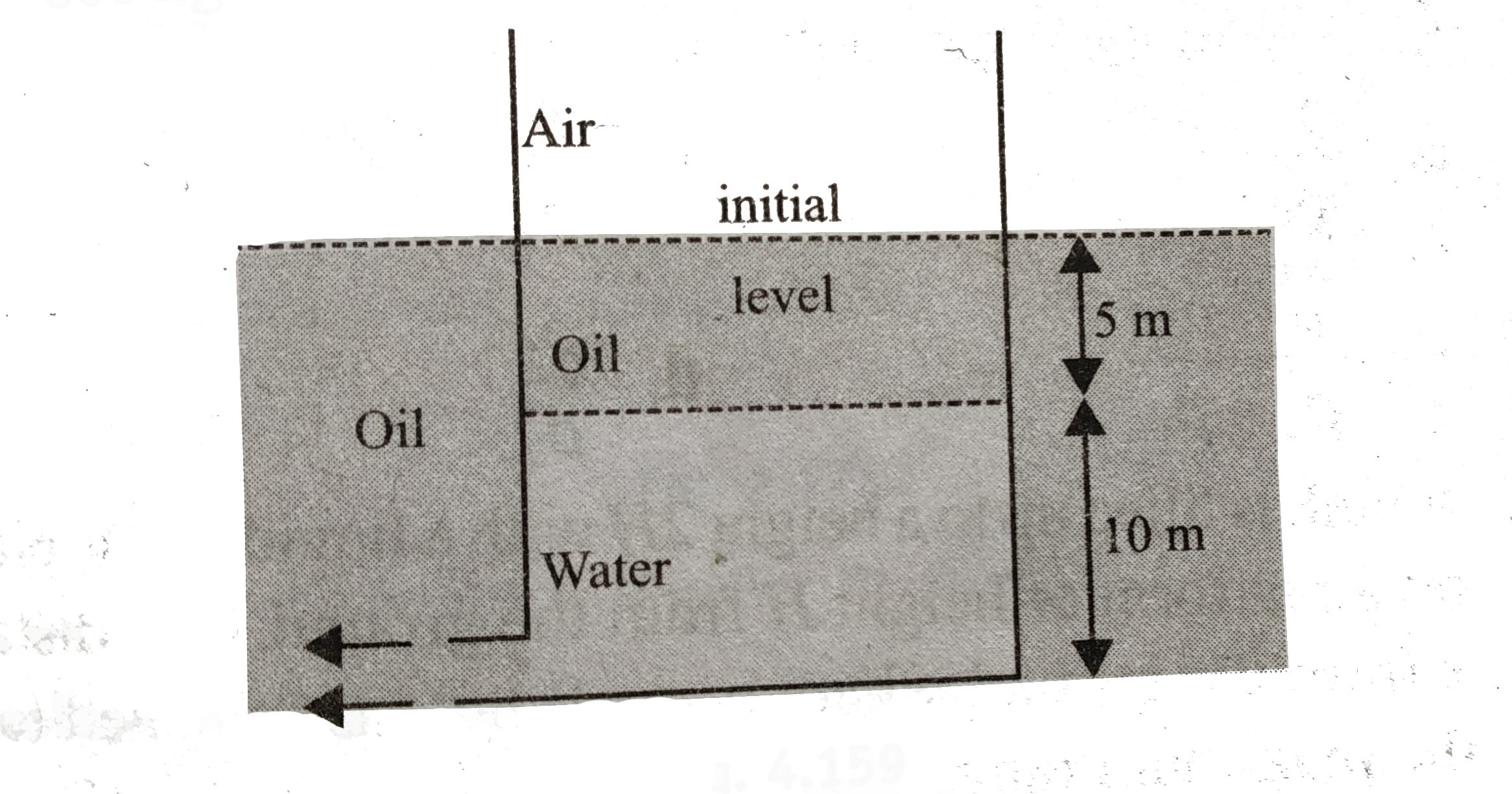
A tank with a small circular hole contains oil on top of water . It is immersed in a larger tank of the same oil . Water flows through the hole .
(a) What is the velocity of this flow intially ?
(b) When the flows stops , what would be the position of the oil - water interface in the tank ? (density of oil = 8 gm/cc)

Applying Bernoulli.s equation between points 1 and 2
⇒Patm+eho0gh0+ρwghw=Patm+ρ0g(h0+hw)+12ρwv2
⇒12ρwv2=ghw(ρw−ρ0)
⇒v=√2ghw(1−ρ0ρw)=√2×9.8×10100(1−8001000)
=0.63 m/s
(b) In the terms of the height h of oil water interface
Patm+ρ0g×5+ρwgh=Patm+ρ0g(10+5)+12ρwv2
⇒12ρwv2=g(ρwh−ρn.10)
Flow stops when ρwh−ρo×10
∴h=0.8×10=8cm
∴ The interface is at a height 8 cm above the base .

Topper's Solved these Questions
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:SOLVED PROBLEMS (OBJECTIVE )
Explore 14 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:LINKED COMPREHENSION TYPE
Explore 2 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT COMPREHENSION NUMERICAL BASED QUESTIONS
Explore 2 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
Similar Questions
A tank with a small orifice contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. Assuming the level of oil outside the tank above orifice does not change. a. What is the velocity of this flow initially? b. When the flow stops, what would be the position of the oil-water interface in the tank? c. Determine the time at which the flow stops. Density,of oil 800kg/m3.
View SolutionA tank with a small orifice contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. Assuming the level of oil outside the tank above orifice does not change.
a. What is the velocity of this flow initially?
b. When the flow stops, what would be the position of the oil-water interface in the tank?
c. Determine the time at which the flow stops. Density,of oil 800kg/m3.

View Solution
Knowledge Check
Water is flowing through a very narrow tube. The velocity of water below which the flow remains a streamline flow is
Arelative velocityBterminal velocityCcritical velocityDparticle velocityIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
Aproportional to hBproportional to h1/2Cproportional to h2Dindependent of hA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2
A water tank has a hole at a distance of 7 m from free water surface. Find the velocity of water through the hole. If the radius of the hole is 2 mm what is the rate of flow of water?
View SolutionWhat is the reason that a constant driving force is always required for the maintenance of the flow of oil through the pipe lines in the oil refineries?
View SolutionTwo holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of 3cm above the bottom, then the distance of the other holes from the top surface of water is
View SolutionThere is a small hole at the bottom of tank filled with water. If total pressure at the bottom is 3atm(1atm=105Nm−2), then find the velocity of water flowing from hole.
View SolutionThe level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View Solution
