The water flowing through the same tube having two different cross section areas has different flow rates .
To determine whether the statement "The water flowing through the same tube having two different cross-sectional areas has different flow rates" is true or false, we can analyze the situation step by step.
Step 1: Understanding Flow Rates
First, we need to clarify what is meant by "flow rates." There are two types of flow rates:
- Volume Flow Rate (Q): This is the volume of fluid that passes through a cross-section per unit time. It is given by the formula:
Q=A⋅v
where A is the cross-sectional area and v is the velocity of the fluid.
- Mass Flow Rate (˙m): This is the mass of fluid that passes through a cross-section per unit time. It is given by:
˙m=ρ⋅Q
where ρ is the density of the fluid.
Step 2: Analyzing the Tube
Consider a tube with two different cross-sectional areas, A1 and A2. According to the principle of conservation of mass (continuity equation), the mass flow rate must remain constant throughout the tube.
Step 3: Applying the Continuity Equation
For an incompressible fluid (like water), the mass flow rate at any two sections of the tube must be equal:
˙m1=˙m2
This means:
ρ⋅Q1=ρ⋅Q2
Since the density ρ remains constant, we can simplify this to:
Q1=Q2
This indicates that the volume flow rate must also be the same at both sections.
Step 4: Conclusion
Since both the mass flow rate and volume flow rate are equal at the two different cross-sectional areas of the tube, we conclude that the statement "The water flowing through the same tube having two different cross-sectional areas has different flow rates" is false.
Final Answer
The statement is false.
---
First, we need to clarify what is meant by "flow rates." There are two types of flow rates:
- Volume Flow Rate (Q): This is the volume of fluid that passes through a cross-section per unit time. It is given by the formula:
Q=A⋅v
where A is the cross-sectional area and v is the velocity of the fluid.
˙m=ρ⋅Q
where ρ is the density of the fluid.
Consider a tube with two different cross-sectional areas, A1 and A2. According to the principle of conservation of mass (continuity equation), the mass flow rate must remain constant throughout the tube.
For an incompressible fluid (like water), the mass flow rate at any two sections of the tube must be equal:
˙m1=˙m2
This means:
ρ⋅Q1=ρ⋅Q2
Since the density ρ remains constant, we can simplify this to:
Q1=Q2
This indicates that the volume flow rate must also be the same at both sections.
Since both the mass flow rate and volume flow rate are equal at the two different cross-sectional areas of the tube, we conclude that the statement "The water flowing through the same tube having two different cross-sectional areas has different flow rates" is false.
The statement is false.
Topper's Solved these Questions
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS (OBJECTIVE ) LEVEL I
40 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS (SUBJECTIVE ) FILL IN THE BLANKS (LEVEL -I)
5 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
Similar Questions
Water is flowing through a horizontal tube having non-uniform area of cross section. If pressure difference between two points along a horizontal tube is 1.5 cm of mercury and speed of flow of water at a point of smaller cross section is 3ms−1, then find the speed of water flow at the other point of larger cross section. Take g=10 m/s2.
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View Solution
Knowledge Check
A fluid of density ρ flows through a horizontal pipe having two different cross-section s of areas A and 2A, Th e pressure at the smaller cross-section is P and lluid velocity at that section is v· What is the velocity and pressure at the larger cross-sect ion
Av2,P+12ρv2Bv4,P+38ρv2Cv2,P+38ρv2Dv,P+34ρv2An ideal liquid (water) flowing through a tube of non-uniform cross section area at A and B are 40cm2 and 20cm2 respectively. If pressure difference between A & B is 700 Nm2 then volume flow rate is
 A2732 cm3sB2142 cm3sC1832 cm3sD3218 cm3s
A2732 cm3sB2142 cm3sC1832 cm3sD3218 cm3sWhen the current i is flowing through a conductor, the drift velocity is v . If 2i current is flowed through the same metal but having double the area of cross-section, then the drift velocity will be
Av/4Bv/2CvD4v
In this figure, an ideal liquid flows through the tube having uniform area of cross-section and is held in vertical plane. Find the ratio of speed of liquid at A and B and also find the pressure difference between- these points.

View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View SolutionWater flows through the tubes shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are 5cm2 and 2cm2 respectively. The rate of flow of water through the tube is 500cm3/s. Find the difference of mercury levels in the U-tube.
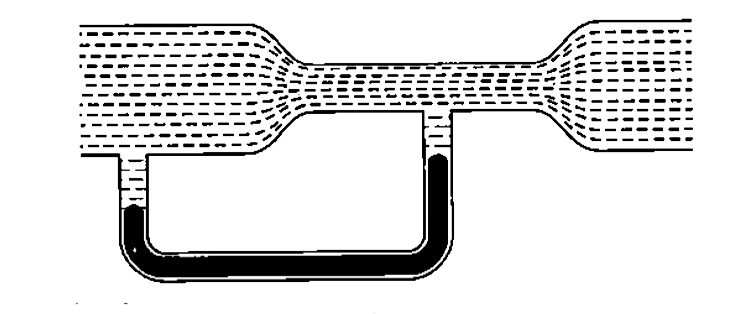
View SolutionWater is flowing through a horizontal tube having crosssectional areas of its two ends being A and A' such that the ratio All' is 5. If the pressure difference of water between the two ends is 3×105Nm−2 the velocity of water with which it enters the tube will be (neglect gravity effects)
View Solutionwater is flowing through a tube of non-uniform cross-section. If the radii of the tube at the ebtrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
View Solution
