Two identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the forces acting on the bases of two identical cylindrical vessels filled with different volumes of water.
1. Identify the Variables:
- Let the base area of both vessels be $A$ .
- Let the height of water in the first vessel be $H_{1}$ .
- Let the height of water in the second vessel be $H_{2}$ .
- We know that $H_{1} > H_{2}$ since the vessels are filled with different volumes of water.
2. Calculate the Pressure at the Base of Each Vessel:
- The pressure at the base of the first vessel (with height $H_{1}$ ) is given by:
$P_{1} = ρ g H_{1}$
- The pressure at the base of the second vessel (with height $H_{2}$ ) is given by:
$P_{2} = ρ g H_{2}$
3. Calculate the Force on the Base of Each Vessel:
- The force on the base of the first vessel is:
$F_{1} = P_{1} \times A = (ρ g H_{1}) \times A$
- The force on the base of the second vessel is:
$F_{2} = P_{2} \times A = (ρ g H_{2}) \times A$
4. Compare the Forces:
- Since $H_{1} > H_{2}$ , it follows that:
$F_{1} = ρ g H_{1} A > F_{2} = ρ g H_{2} A$
- Therefore, $F_{1}$ is greater than $F_{2}$ .
5. Conclusion:
- The statement that the forces on the bases of the two vessels are the same is false. The force on the base of the vessel with greater height of water will be greater.
Final Answer:
The statement is false.

Updated on:18/9/2024

Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density $ρ$ . The area of either base is A but in one vessel the liquid height is $h_{1}$ and in the other liquid height is $h_{2} (h_{2} < h_{1})$ . If the two vessel are connected, the work done by gravity in equalizing the level is
A $\frac{1}{2} {(h_{1} - h_{2})}_{1}^{2} A ρ g$
B $\frac{1}{2} {(h_{1} + h_{2})}_{1}^{2} A ρ g$
C $\frac{1}{2} {(h_{1}^{2} - h_{2}^{2})}^{2} A ρ g$
D $\frac{1}{4} {(h_{1} - h_{2})}_{1}^{2} A ρ g$
Two vessels $A$ and $B$ of different shapes have the same base area and are filled with water up to the same height $h$ (see figure). The force exerted by water on the base is $F_{A}$ for vessel $A$ and $F_{B}$ for vessel $B$ . The respective weights of the water filled in vessels are $W_{A}$ and $W_{B}$ . Then

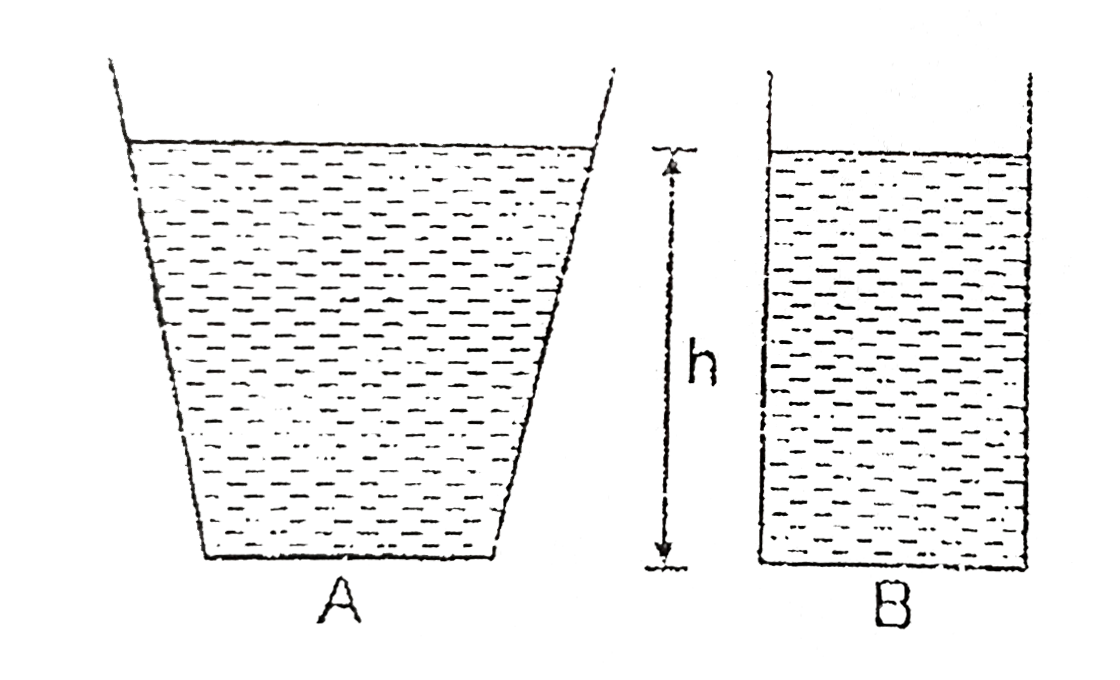A $F_{A} > F_{B}, W_{A} > W_{B}$
B $F_{A} = F_{B}, W_{A} > W_{B}$
C $F_{A} = F_{B}, W_{A} < W_{B}$
D $F_{A} > F_{B}, W_{A} = W_{B}$
A liquid of density $ρ$ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is $h_{1}$ and that in the other vessel is $h_{2}$ . If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
A $(h_{1} - h_{2}) g ρ$
B $(h_{1} - h_{2}) g A ρ$
C $\frac{1}{2} {(h_{1} - h_{2})}_{1}^{2} g A ρ$
D $\frac{1}{4} {(h_{1} - h_{2})}_{1}^{2} g A ρ$