A block B of specific gravity 2 and another block C of specific gravity 0.5 .Both are joined together and they are floating water such that they are completely dipped inside water , the ratio of the masses of the blocks B and C is
2:1
3:2
5:3
2:3
The correct Answer is:A
To find the ratio of the masses of blocks B and C, we can follow these steps:
Step 1: Understand the Specific Gravity
Specific gravity is defined as the ratio of the density of a substance to the density of water.
- For block B (specific gravity = 2), the density ρB=2⋅ρw
- For block C (specific gravity = 0.5), the density ρC=0.5⋅ρw
Step 2: Apply the Floating Condition
When the blocks are floating, the total weight of the blocks must equal the buoyant force acting on them. The buoyant force is equal to the weight of the water displaced, which can be expressed as:
Buoyant Force=ρw⋅g⋅(VB+VC)
where VB and VC are the volumes of blocks B and C, respectively.
Step 3: Relate Volume to Mass
The volume of each block can be expressed in terms of mass and density:
VB=mBρBandVC=mCρC
Step 4: Set Up the Equation
From the floating condition, we have:
mBg+mCg=ρwg(VB+VC)
Cancelling g from both sides gives:
mB+mC=ρw(mBρB+mCρC)
Step 5: Substitute Densities
Substituting the expressions for ρB and ρC:
mB+mC=ρw(mB2ρw+mC0.5ρw)
This simplifies to:
mB+mC=mB2+2mC
Step 6: Rearranging the Equation
Rearranging gives:
mB+mC−mB2−2mC=0
This can be rewritten as:
12mB−mC=0
or
12mB=mC
Step 7: Finding the Ratio
From the equation mC=12mB, we can express the ratio of the masses:
mBmC=2
Final Answer
Thus, the ratio of the masses of block B to block C is:
mBmC=2:1
Specific gravity is defined as the ratio of the density of a substance to the density of water.
- For block B (specific gravity = 2), the density ρB=2⋅ρw
- For block C (specific gravity = 0.5), the density ρC=0.5⋅ρw
When the blocks are floating, the total weight of the blocks must equal the buoyant force acting on them. The buoyant force is equal to the weight of the water displaced, which can be expressed as:
Buoyant Force=ρw⋅g⋅(VB+VC)
where VB and VC are the volumes of blocks B and C, respectively.
The volume of each block can be expressed in terms of mass and density:
VB=mBρBandVC=mCρC
From the floating condition, we have:
mBg+mCg=ρwg(VB+VC)
Cancelling g from both sides gives:
mB+mC=ρw(mBρB+mCρC)
Substituting the expressions for ρB and ρC:
mB+mC=ρw(mB2ρw+mC0.5ρw)
This simplifies to:
mB+mC=mB2+2mC
Rearranging gives:
mB+mC−mB2−2mC=0
This can be rewritten as:
12mB−mC=0
or
12mB=mC
From the equation mC=12mB, we can express the ratio of the masses:
mBmC=2
Thus, the ratio of the masses of block B to block C is:
mBmC=2:1
Topper's Solved these Questions
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS (OBJECTIVE ) ASSERTION REASONING TYPE LEVEL -I
1 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS (OBJECTIVE ) ASSERTION REASONING TYPE LEVEL-I
1 Videos
- FLUID MECHANICS BOOK - FIITJEECHAPTER - FLUID MECHANICS EXERCISE - ASSIGHNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- ELECTROSTATICSBOOK - FIITJEECHAPTER - ELECTROSTATICSEXERCISE - Example
14 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
Similar Questions
An object floats in water such that half of its volume is immersed in it. The specific gravity of the object is _____.
View SolutionA block of wood weighing 71.2N and of specific gravity 0.75 is tied by a string to the bottom of a tank of water in order to have the block totally immersed, What is the tension in the string?
View Solution
Knowledge Check
A cubical block of wood of specific gravity 0.5 and chunk of concrete of specific gravity 2.5 are fastened together the ratio of mass of wood to the mass of concrete which makes the combination to float with entire volume of the combination submerged in water is
A1/5B1/3C3/5D2/5A block weighs 15 N in air and 12 N.when immersed in water. The specific gravity of the block is
A0.8B0.25C5/4D5A liquid A of specific heat 0.5 at 60∘C is mixed with another liquid B of specific heat 0.3 at 20∘C. After mixing, the resultant temperature of the mixture is 30∘C. The ratio of masses of A and B respectively is
A1:2B1:3C1:5D2:3
A block of ice is floating in a liquid of specific gravity 1.2 contained in the beaker. What will be the effect on the level of liquid in the beaker when the whole ice melts?
View SolutionA cubical block of wood weighing 200g has a lead piece fastened underneath. Find the mass of the lead pieces which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
(b) Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
View SolutionA block of ice is floating in a glass containing water .When the ice melts completely ,the level of the water in the glass will :
View SolutionA block of ice is floating in a liquid of specific gravity 1.2 contained in a beaker. What will happen to the liquid level when ice completely melts?
View Solution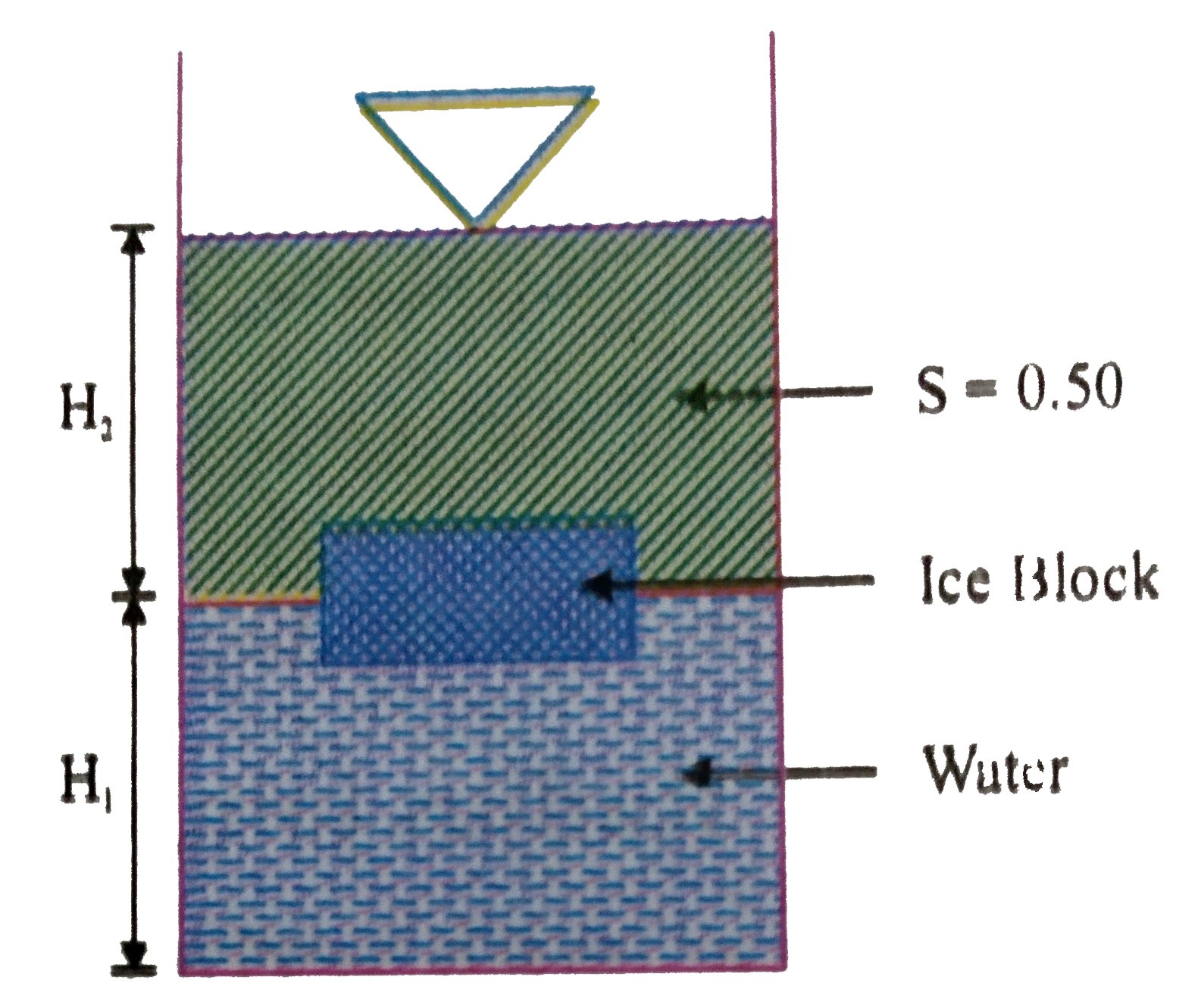
A block of ice (specified gravity Si−=0.90) is floating in a container having two immiscible liquids (one of specific gravity S=0.50 and other is water) as shown in the figure. (H,H2 are height of water other liquid columns respectively). Now the ice block melts completely,then
View Solution
