The gravitational field strength $\to E$ and gravitational potential $V$ are releated as
$\to E = - (\frac{δ V}{δ x} ˆ i + \frac{δ V}{δ y} ˆ j + \frac{δ V}{δ z} ˆ k)$

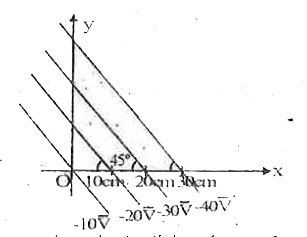
In the figure, transversal lines represent equipotential surfaces. A particle of mass $m$ is released from rest at the origin. The gravitational unit of potential , $1 \to V = 1 c m^{2} / s^{2}$
$y$ -component of $E$ a the point whose co-ordinates are $(4 c m, 4 c m)$ is

$1 c m / s^{2}$

$8 c m / s^{2}$

$4 c m / s^{2}$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for The gravitational field strength vecE and gravitational potential V are releated as vecE=-((deltaV)/(deltax)hati+(deltaV)/(deltay)hatj+(deltaV)/(deltaz)hatk) In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1vecV=1cm^(2)//s^(2) y-component of E a the point whose co-ordinates are (4cm,4cm) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
The gravitational field strength $\to E$ and gravitational potential $V$ are releated as
$\to E = - (\frac{δ V}{δ x} ˆ i + \frac{δ V}{δ y} ˆ j + \frac{δ V}{δ z} ˆ k)$

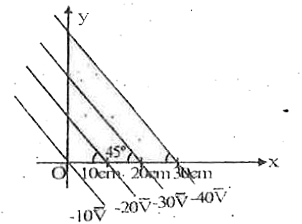
In the figure, transversal lines represent equipotential surfaces. A particle of mass $m$ is released from rest at the origin. The gravitational unit of potential , $1 \to V = 1 c m^{2} / s^{2}$
$x$ -component of the velocity of the particle at the point $(4 c m, 4 c m)$ is
A $4 c m / s$
B $2 c m / s$
C $2 \sqrt{2} \frac{c m}{s}$
D $1 c m / s$
Question 2 - Select One
The gravitational field strength $\to E$ and gravitational potential $V$ are releated as
$\to E = - (\frac{δ V}{δ x} ˆ i + \frac{δ V}{δ y} ˆ j + \frac{δ V}{δ z} ˆ k)$

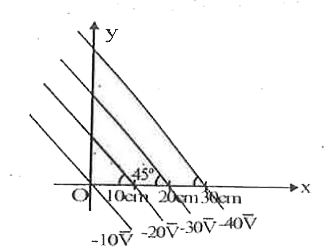
In the figure, transversal lines represent equipotential surfaces. A particle of mass $m$ is released from rest at the origin. The gravitational unit of potential , $1 \to V = 1 c m^{2} / s^{2}$
$x$ -component of the velocity of the particle at the point $(4 c m, 4 c m)$ is
A $4 c m / s$
B $2 c m / s$
C $2 \sqrt{2} \frac{c m}{s}$
D $1 c m / s$
Question 3 - Select One
The gravitational field strength $\to E$ and gravitational potential $V$ are releated as
$\to E = - (\frac{δ V}{δ x} ˆ i + \frac{δ V}{δ y} ˆ j + \frac{δ V}{δ z} ˆ k)$

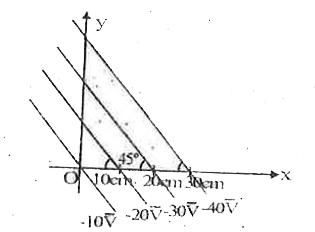
In the figure, transversal lines represent equipotential surfaces. A particle of mass $m$ is released from rest at the origin. The gravitational unit of potential , $1 \to V = 1 c m^{2} / s^{2}$
Speed of the particle $(v)$ ( $y$ is in cm and v in cm/s) as function of its $y$ -co-ordinate is
A $v = 2 \sqrt{y}$
B $v = \sqrt{2} y$
C $v = 2 y$
D $v = 2 y + 4 y^{2} + 2 y^{2}$

FIITJEE-GRAVITATION-Comprehension

Home
Ask Doubt
Profile

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

FIITJEE-GRAVITATION-Comprehension