The gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
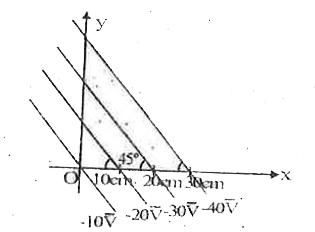
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v in cm/s) as function of its y-co-ordinate is
v=2√y
v=√2y
v=2y
v=2y+4y2+2y2
The correct Answer is:A
Step by step video, text & image solution for The gravitational field strength vecE and gravitational potential V are releated as vecE=-((deltaV)/(deltax)hati+(deltaV)/(deltay)hatj+(deltaV)/(deltaz)hatk) In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1vecV=1cm^(2)//s^(2) Speed of the particle (v) (y is in cm and v in cm/s) as function of its y-co-ordinate is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assertion & Reasoning type1videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Questions4videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Solved problem (Objective)15videos
GRAVITATION
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
Similar Questions
Assertion : Gravitational potential of earth at every place on it is negative.
Reason : Every body on earth is bound by the attraction of earth.02:04View SolutionA pendulum clock, which keeps correct time at sea level, loses 15s per day when taken to the top of a mountain. If the radius of the earth is 6400km, the height of the mountain is
02:03View SolutionA particle hanging from a spring stratches it by 1cm at earth's surface. Radius of the earth is 6400km. At a place 800km above the earth's surface, the same particle will stretch the spring by
08:22View SolutionA cyclist is going in a straight line at a unifrom velocity 18km/h. The resistance force can be expressed as force kv2 where k=0.8 where velocity is in m/s and unit of force is newton. The mass of the cyclist with the bicycle is 100kg. Neglect the rolling resistance force. If the power of the cyclist during the ride is 10x watt, then what is x ?
08:22View SolutionEnds of two wires A and B, having resistivityρA=3×105Ωm and ρB=6×10−5ωm of same cross section ara are pointed together to form a single wire. If the resistance of the joined wire does not change with temperature, then find the ratio of their lengths given that temperatue coefficient of resistitivy of wires A and B are α=4×10−5/∘C and α=−4×106/∘C . Assume that mechanical dimensions do not change with temperature.
08:22View SolutionGravitational potential in x−y plan varies with x and y
coordinates as
V=x2y+2xy
Find gravitational field strength E.07:52View SolutionThe gravitational field in a region is given by vecE=-(20Nkg^(-1))(hati+hatj) . Find the gravitational potential at the origin (0,0) in J kg^(-1)
03:45View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V = 2x^2 , where x is in meter. Its variation is as shown in figure Draw the variation of electric field (E ) along the x-axis.
04:23View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V = 2x^2 , where x is in meter. Its variation is as shown in figure A charge particle of mass 10 mg and charge 2.5 muC is released from rest at x = 2 m . Find its velocity when it crosses origin.
04:23View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation vecE = - (deltaV)/(deltax)hati - (deltaV)/(deltay)hatj - (deltaV)/(deltaz)hatk if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V = 2x^2 , where x is in meter. Its variation is as shown in figure Will the particle perform a simple harmonic motion? Also, find the time period of its oscillations.
View Solution(a) If gravitational field is given by vecE=-2xhati-3y^(2)hatj . If gravitational potential is zero at (0,0) , find potential at (1,2) (b) If gravitational potential is V=x^(2)Y , find gravitational field at (1,2) .
View SolutionThe gravitational field strength vecE and gravitational potential V are releated as vecE=-((deltaV)/(deltax)hati+(deltaV)/(deltay)hatj+(deltaV)/(deltaz)hatk) In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1vecV=1cm^(2)//s^(2) y -component of E a the point whose co-ordinates are (4cm,4cm) is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
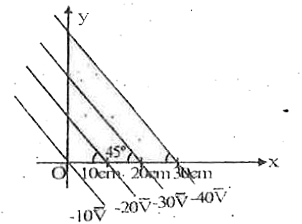
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) is03:14View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
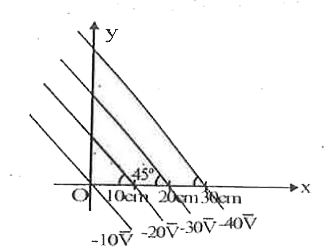
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) is02:21View SolutionA particle of mass 4g is in a gravitational potential field given by V= (800x^(2)+150)erg"/"g . Its frequency of oscillations is
03:02View SolutionA particle of mass 4g is in a gravitational potential field given by V=(800x2+150)erg/g. Its frequency of oscillations is
01:41View Solution

