A thin hollow sphere of mass m=2kg, radius=(1/2)m is sliding on a horizontal surface with a constant frequency n = 60 rpm. Find the total mechanical energy of the hollow sphere.
To find the total mechanical energy of a thin hollow sphere sliding on a horizontal surface, we need to consider both its translational and rotational kinetic energies. Here’s a step-by-step solution:
Step 1: Identify the Given Values
- Mass of the hollow sphere, m=2kg
- Radius of the hollow sphere, r=12m
- Frequency, n=60rpm
Step 2: Convert Frequency to Angular Velocity
First, we need to convert the frequency from revolutions per minute (rpm) to radians per second (rad/s).
ω=2π×(n60)=2π×(6060)=2πrad/s
Step 3: Calculate the Translational Kinetic Energy
The translational kinetic energy (TKE) of the hollow sphere is given by:
TKE=12mv2
Where v is the linear velocity. The linear velocity v can be related to the angular velocity ω and the radius r:
v=rω=12×2π=πm/s
Now substituting v into the TKE formula:
TKE=12×2×(π)2=π2J
Step 4: Calculate the Moment of Inertia
The moment of inertia I for a thin hollow sphere is given by:
I=23mr2
Substituting the values:
I=23×2×(12)2=23×2×14=13kg m2
Step 5: Calculate the Rotational Kinetic Energy
The rotational kinetic energy (RKE) is given by:
RKE=12Iω2
Substituting I and ω:
RKE=12×13×(2π)2=16×4π2=2π23J
Step 6: Calculate Total Mechanical Energy
The total mechanical energy E is the sum of the translational and rotational kinetic energies:
E=TKE+RKE=π2+2π23
To combine these, convert π2 to a common denominator:
E=3π23+2π23=5π23J
Step 7: Numerical Evaluation
Using π≈3.14:
E≈5×(3.14)23≈5×9.85963≈49.2983≈16.43J
Conclusion
The total mechanical energy of the hollow sphere is approximately 16.43J.
---
- Mass of the hollow sphere, m=2kg
- Radius of the hollow sphere, r=12m
- Frequency, n=60rpm
First, we need to convert the frequency from revolutions per minute (rpm) to radians per second (rad/s).
The translational kinetic energy (TKE) of the hollow sphere is given by:
The moment of inertia I for a thin hollow sphere is given by:
The rotational kinetic energy (RKE) is given by:
The total mechanical energy E is the sum of the translational and rotational kinetic energies:
Using π≈3.14:
The total mechanical energy of the hollow sphere is approximately 16.43J.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)10videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)14videos
ROTATIONAL MECHANICS
- BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type6videos
PHYSICS PART2
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
Similar Questions
A solid sphere of mass m and radius R rolls without slipping on the horizontal surface such that its velocity of center of mass is v0. Find its translational kinetic energy, rotational kinetic energy, total kinetic energy, gravitational potential energy taking surface as reference level and mechanical energy.
View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
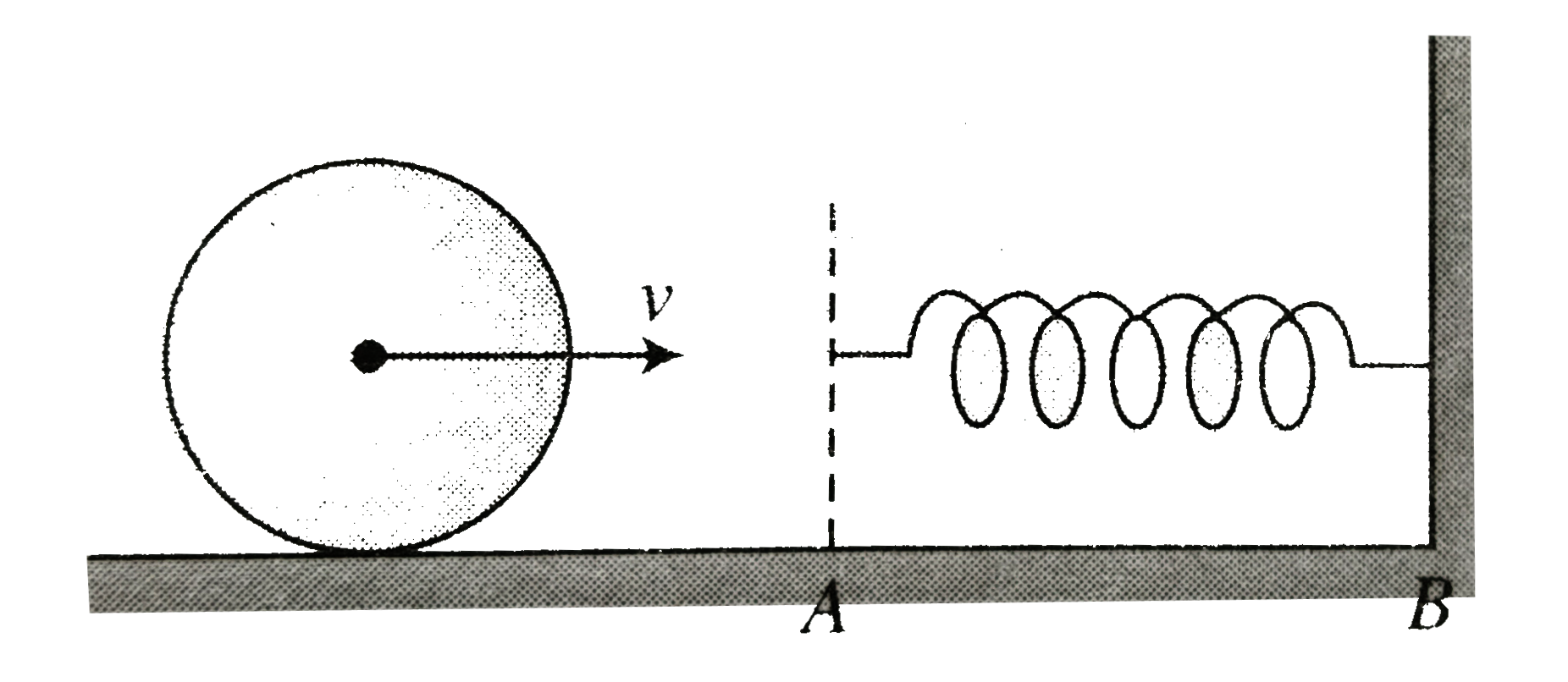 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
A0.014 JB0.028 JC14 JD28 J - Question 2 - Select One
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
A0.014 JB0.028 JC14 JD28 J - Question 3 - Select One
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.
A sphere of mass 0.5 kg and diameter 1 m rolls without sliding with a constant velocity of 5 m/s. What is the ratio of rotational KE to the total kinetic energy of the sphere ?
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
View SolutionA point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
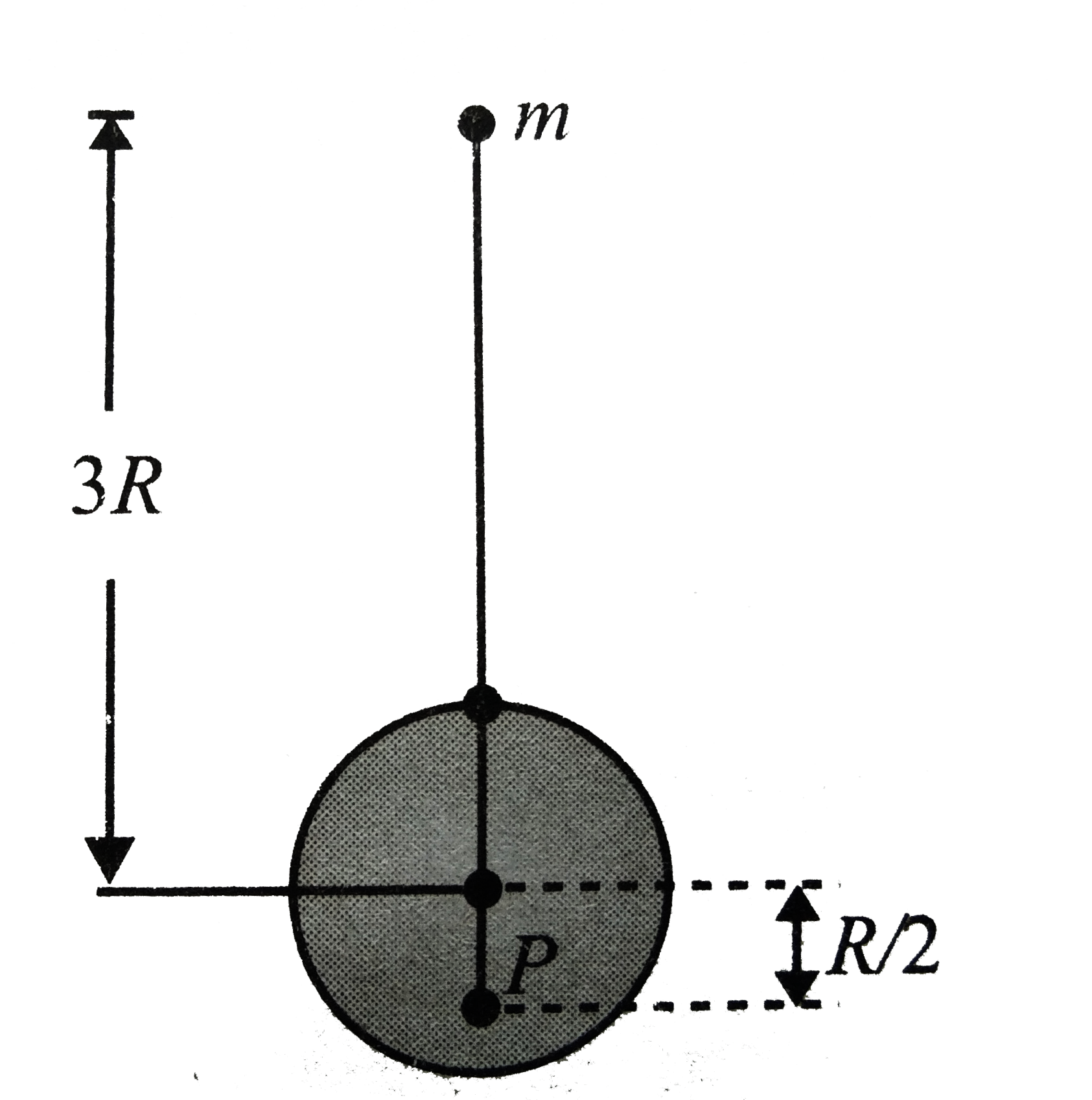 View Solution
View SolutionA uniform solid sphere A of mass m is rolling without sliding on a a smooth horizontal surface. It collides elastically and head - on with another stationary hollow sphere B of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of B to that of A just after the collision is
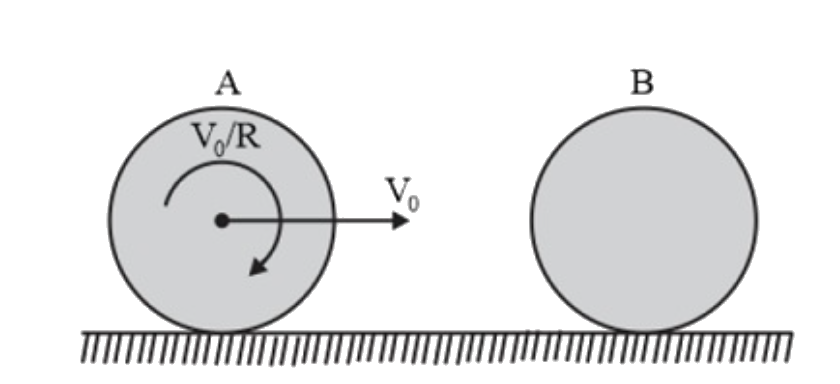 View Solution
View SolutionA solid homogenous sphere of mass M and radius r is moving on a rough horizontal surface, partly rolling and partly sliding. During this kind of motion of this sphere
View Solution

